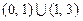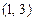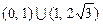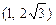题目内容
设函数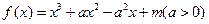 .
.
(1)若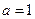 时函数
时函数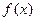 有三个互不相同的零点,求
有三个互不相同的零点,求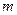 的取值范围;
的取值范围;
(2)若函数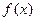 在
在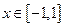 内没有极值点,求
内没有极值点,求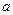 的取值范围;
的取值范围;
(3)若对任意的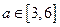 ,不等式
,不等式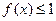 在
在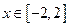 上恒成立,求实数
上恒成立,求实数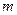 的取值范围.
的取值范围.
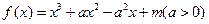 .
.(1)若
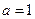 时函数
时函数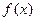 有三个互不相同的零点,求
有三个互不相同的零点,求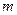 的取值范围;
的取值范围;(2)若函数
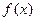 在
在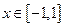 内没有极值点,求
内没有极值点,求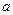 的取值范围;
的取值范围;(3)若对任意的
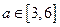 ,不等式
,不等式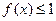 在
在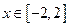 上恒成立,求实数
上恒成立,求实数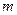 的取值范围.
的取值范围.(1)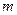 的取值范围是
的取值范围是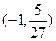 ;(2)
;(2)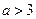 ;(3)
;(3)
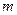 的取值范围是
的取值范围是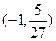 ;(2)
;(2)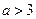 ;(3)
;(3)
(1)当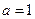 时
时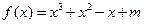 ,
,
∵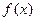 有三个互不相同的零点,
有三个互不相同的零点,
∴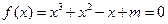 即
即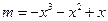 有三个互不相同的实数根.
有三个互不相同的实数根.
令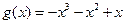 ,则
,则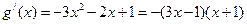
∵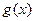 在
在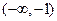 和
和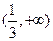 均为减函数,在
均为减函数,在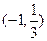 为增函数,
为增函数,
∴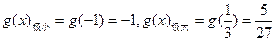
所以 的取值范围是
的取值范围是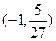
(2)由题设可知,方程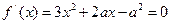 在
在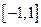 上没有实数根,
上没有实数根,
∴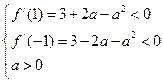 ,解得
,解得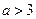
(3)∵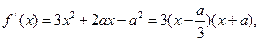 又
又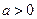 ,
,
∴当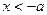 或
或 时,
时,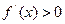 ;当
;当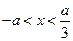 时,
时,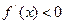 .
.
∴函数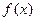 的递增区间为
的递增区间为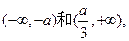 单调递减区间为
单调递减区间为
当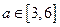 时,
时, 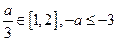 , 又
, 又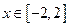 ,∴
,∴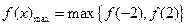
而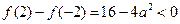 ,∴
,∴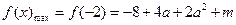 ,
,
又∵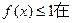
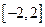 上恒成立,∴
上恒成立,∴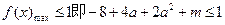 ,
,
即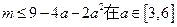 上恒成立.
上恒成立.
∵ 的最小值为
的最小值为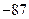 , ∴
, ∴
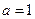 时
时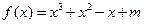 ,
,∵
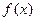 有三个互不相同的零点,
有三个互不相同的零点,∴
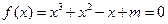 即
即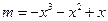 有三个互不相同的实数根.
有三个互不相同的实数根.令
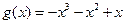 ,则
,则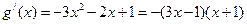
∵
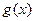 在
在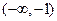 和
和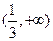 均为减函数,在
均为减函数,在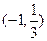 为增函数,
为增函数,∴
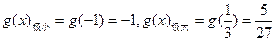
所以
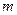 的取值范围是
的取值范围是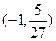
(2)由题设可知,方程
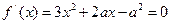 在
在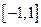 上没有实数根,
上没有实数根,∴
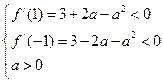 ,解得
,解得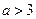
(3)∵
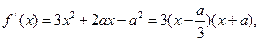 又
又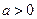 ,
,∴当
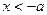 或
或 时,
时,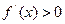 ;当
;当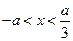 时,
时,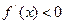 .
.∴函数
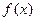 的递增区间为
的递增区间为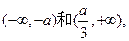 单调递减区间为
单调递减区间为
当
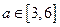 时,
时, 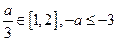 , 又
, 又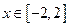 ,∴
,∴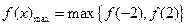
而
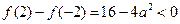 ,∴
,∴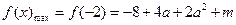 ,
,又∵
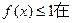
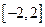 上恒成立,∴
上恒成立,∴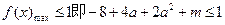 ,
,即
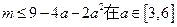 上恒成立.
上恒成立.∵
 的最小值为
的最小值为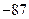 , ∴
, ∴

练习册系列答案
相关题目
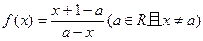
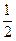 ,a+1]时,求证:f(x)的值域为[-3,-2];
,a+1]时,求证:f(x)的值域为[-3,-2]; ,已知
,已知 时,
时, 有最小值
有最小值 ,
, 与
与 的值;(2)在(1)的条件下,求
的值;(2)在(1)的条件下,求 的解集
的解集 ;
; ,且
,且 ,求实数
,求实数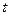 的取值范围
的取值范围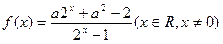 ,其中a为常数,且
,其中a为常数,且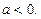
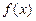 是奇函数,求a的取值集合A;
是奇函数,求a的取值集合A;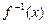 ,且函数
,且函数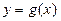 的图像与
的图像与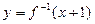 的图像关于
的图像关于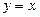 对称,求
对称,求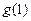 的取值集合B。
的取值集合B。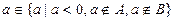 时,不等式
时,不等式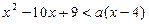 恒成立,求x的取值范围。
恒成立,求x的取值范围。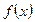 的定义域为实数集
的定义域为实数集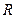 ,且
,且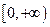 上是增函数,当
上是增函数,当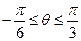 时,是否存在实数
时,是否存在实数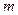 ,使
,使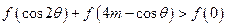 对所有的
对所有的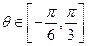 恒成立?若存在,求出实数
恒成立?若存在,求出实数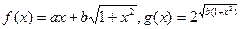 ,且
,且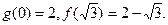
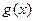 的值域;
的值域;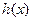 满足
满足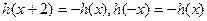 ,且当
,且当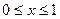 时
时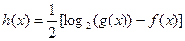 ,求
,求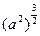 =a3 ②
=a3 ②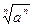 =|a| ③函数y=
=|a| ③函数y=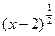 -(3x-7)0的定义域是(2, +∞) ④若
-(3x-7)0的定义域是(2, +∞) ④若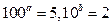 ,则2a+b=1
,则2a+b=1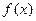 的解析式;(2)用定义证明
的解析式;(2)用定义证明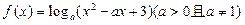 ,满足对任意的
,满足对任意的 、
、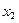 ,当
,当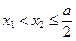 时,
时,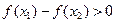 ,则实数
,则实数 的取值范围为( )
的取值范围为( )