Question

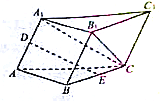
【题目】三棱锥P﹣ABC中，PO⊥面ABC，垂足为O，若PA⊥BC，PC⊥AB，求证：
（1）AO⊥BC
（2）PB⊥AC．

Answer 1

【答案】
（1）证明：∵PO⊥平面ABC，

又BC平面ABC，

∴PO⊥BC

又PA⊥BC，PO∩PA=P，

∴BC⊥平面PAO

∵AO平面PAO

∴AO⊥BC

（2）证明：PO⊥面ABC，垂足为O，PA⊥BC，PC⊥AB，则OA⊥BC，OC⊥AB，又三角形的高交于一点，∴BO⊥AC，∴PB⊥AC
【解析】（1）要证AO⊥BC，只需要证BC⊥平面PAO，要只需要证PO⊥BC，PA⊥BC，只需要证PA⊥平面PBC，根据已知条件可证；（2）利用三垂线定理以及三角形的高 交于一点得证．
【考点精析】通过灵活运用直线与平面垂直的性质，掌握垂直于同一个平面的两条直线平行即可以解答此题．