题目内容
17.已知x>0,则函数y=$\frac{4{x}^{2}-x+1}{x}$的最小值为3.分析 变形已知式子可得y=$\frac{4{x}^{2}-x+1}{x}$=4x+$\frac{1}{x}$-1,由基本不等式可得.
解答 解:由题意可得x>0,
∴y=$\frac{4{x}^{2}-x+1}{x}$=4x+$\frac{1}{x}$-1
≥2$\sqrt{4x•\frac{1}{x}}$-1=3
当且仅当4x=$\frac{1}{x}$即x=$\frac{1}{2}$时取等号,
故答案为:3
点评 本题考查基本不等式求最值,化为可利用基本不等式的形式是解决问题的关键,属基础题.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案
相关题目
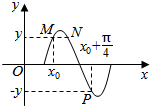 若函数f(x)=sin(ωx+φ)(ω>0,-π<φ<0)的部分图象如图所示.
若函数f(x)=sin(ωx+φ)(ω>0,-π<φ<0)的部分图象如图所示.