题目内容
5.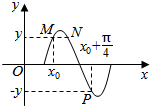 若函数f(x)=sin(ωx+φ)(ω>0,-π<φ<0)的部分图象如图所示.
若函数f(x)=sin(ωx+φ)(ω>0,-π<φ<0)的部分图象如图所示.(1)求ω的值.
(2)若x0=$\frac{π}{4}$,且M、N、P三点的横坐标成等差数列,已知△ABC的三边满足b2=ac,求f(B)的取值范围.
分析 (1)首先,根据函数的图象,得到该函数的周期,然后,确定ω的值;
(2)结合所给三点成等差数列,得到xN=$\frac{3π}{8}$,然后,确定φ=-$\frac{π}{4}$,最后,求解范围即可.
解答 解:(1)根据图象,得
$\frac{T}{2}=\frac{π}{4}$,
∴T=$\frac{π}{2}$,
∴$\frac{2π}{ω}=\frac{π}{2}$,
∴ω=4,
(2)∵x0=$\frac{π}{4}$,
∴xM=$\frac{π}{4}$,xP=$\frac{π}{2}$,
∵M、N、P三点的横坐标成等差数列,
∴2xN=xM+xP,
∴xN=$\frac{3π}{8}$,
∴sin(4×$\frac{π}{4}+$φ)=sin($4×\frac{3π}{8}$+φ)
∴-sinφ=cosφ,
∴tanφ=-1,
∵-π<φ<0,
∴φ=-$\frac{π}{4}$,
∴f(x)=sin(4x-$\frac{π}{4}$)
∵b2=ac,
∴cosB=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$
≥$\frac{2ac-ac}{2ac}$=$\frac{1}{2}$,
∴0<B≤$\frac{π}{3}$,
∴0<4B$≤\frac{4π}{3}$,
∴-$\frac{π}{4}$<4B-$\frac{π}{4}$≤$\frac{13π}{12}$,
∵f(B)=sin(4B-$\frac{π}{4}$),
∴-$\frac{\sqrt{2}}{2}$<f(B)≤1,
∴f(B)的取值范围(-$\frac{\sqrt{2}}{2}$,1].
点评 本题考查由y=Asin(ωx+φ)的部分图象确定解析式、函数y=Asin(ωx+φ)的图象变换,考查函数方程思想、数形结合思想.

 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | 1 |
 已知某几何体的三视图如图所示,分别为正方形、直角三角形、等腰三角形(单位:cm),则该几何体的体积是( )
已知某几何体的三视图如图所示,分别为正方形、直角三角形、等腰三角形(单位:cm),则该几何体的体积是( )| A. | $\frac{8}{3}$cm3 | B. | 8cm3 | C. | 4cm3 | D. | $\frac{8\sqrt{5}}{3}$cm3 |