题目内容
12.计算下列曲线所围成的面积(1)y=x2,y=x+2;
(2)y2=2x+1,y2=-2x+1.
分析 分别画出曲线围成的图形,利用定积分表示图形面积,然后计算即可.
解答 解:(1)y=x2,y=x+2围成图形如图,面积为
${∫}_{-1}^{2}(x+2-{x}^{2})dx$=($\frac{1}{2}{x}^{2}$+2x-$\frac{1}{3}{x}^{3}$)|${\;}_{-1}^{2}$=$\frac{9}{2}$;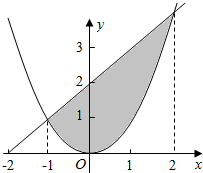
(2)解:y2=2x+1,y2=-2x+1围成的图形如图,面积为4${∫}_{0}^{1}(\frac{1}{2}-\frac{{y}^{2}}{2})dy$=$\frac{4}{3}$.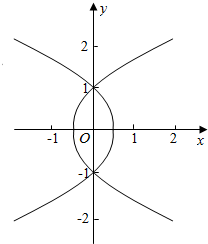
点评 本题求曲线围成的曲边图形的面积,着重考查了定积分的几何意义和积分计算公式等知识,灵活选择积分变量比较关键.

练习册系列答案
相关题目
4.设a>|b|,且b<0,则( )
| A. | a+b>0 | B. | a+b<0 | C. | |a|<|b| | D. | b-a>0 |
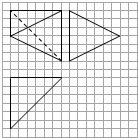 已知某几何体的三视图如图所示,求该几何体的体积.
已知某几何体的三视图如图所示,求该几何体的体积.