题目内容
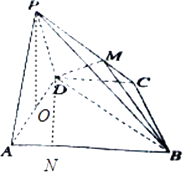
【题目】如图所示,在四棱锥P﹣ABCD中,平面PAD⊥平面ABCD,AB∥DC,△PAD是等边三角形,已知BD=8,AD=4,AB=2DC=4 ![]() .
. 
(1)设M是PC上的一点,求证:平面MBD⊥平面PAD;
(2)求四棱锥P﹣ABCD的体积.
【答案】
(1)证明:在△ABD中,∵AD=4,AB=4 ![]() ,BD=8,
,BD=8,
∴AD2+BD2=AB2,
∴AD⊥BD.
又∵面PAD⊥面ABCD,平面PAD∩平面ABCD=AD,BD平面ABCD,
∴BD⊥面PAD,
又BD面BDM,
∴面MBD⊥面PAD
(2)解:过P作PO⊥AD,
∵面PAD⊥面ABCD,面PAD∩面ABCD=AD,PO平面PAD,
∴PO⊥面ABCD,
即PO为四棱锥P﹣ABCD的高.
又△PAD是边长为4的等边三角形,
∴PO=2 ![]() .
.
过D作DN⊥AB,则DN= ![]() =
= ![]() .
.
∴S梯形ABCD= ![]() ×(2
×(2 ![]() +4
+4 ![]() )×
)× ![]() =24,
=24,
∴VP﹣ABCD= ![]() =16
=16 ![]() .
.
【解析】(1)利用勾股定理逆定理可得AD⊥BD,根据面面垂直的性质得出BD⊥平面PAD,故而平面BDM⊥平面PAD;(2)过P作PO⊥AD,则PO⊥平面ABCD,求出梯形ABCD的高和棱锥的高PO,代入棱锥的体积公式计算即可.
【考点精析】认真审题,首先需要了解平面与平面垂直的判定(一个平面过另一个平面的垂线,则这两个平面垂直).

 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案【题目】在某城市气象部门的数据中,随机抽取了100天的空气质量指数的监测数据如表:
空气质量指数t | (0,50] | (50,100] | (100,150] | (150,200] | (200,300] | (300,+∞) |
质量等级 | 优 | 良 | 轻微污染 | 轻度污染 | 中度污染 | 严重污染 |
天数K | 5 | 23 | 22 | 25 | 15 | 10 |
(1)在该城市各医院每天收治上呼吸道病症总人数y与当天的空气质量t(t取整数)存在如下关系y= ![]() ,且当t>300时,y>500估计在某一医院收治此类病症人数超过200人的概率;
,且当t>300时,y>500估计在某一医院收治此类病症人数超过200人的概率;
(2)若在(1)中,当t>300时,y与t的关系拟合于曲线 ![]() ,现已取出了10对样本数据(ti , yi)(i=1,2,3,…,10),且
,现已取出了10对样本数据(ti , yi)(i=1,2,3,…,10),且 ![]() =42500,
=42500, ![]() =500,求拟合曲线方程. (附:线性回归方程
=500,求拟合曲线方程. (附:线性回归方程 ![]() =a+bx中,b=
=a+bx中,b= ![]() ,a=
,a= ![]() ﹣b
﹣b ![]() )
)

