题目内容
【题目】抛物线y2=2px（p＞0）的焦点为F，已知点A，B为抛物线上的两个动点，且满足∠AFB=120°．过弦AB的中点M作抛物线准线的垂线MN，垂足为N，则 
的最大值为 ．
【答案】
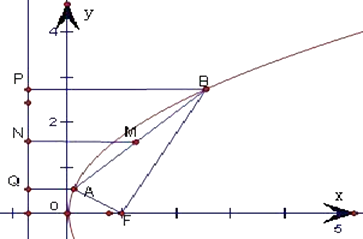
【解析】解：设|AF|=a，|BF|=b，连接AF、BF，
由抛物线定义，得|AF|=|AQ|，|BF|=|BP|，
在梯形ABPQ中，2|MN|=|AQ|+|BP|=a+b．
由余弦定理得，
|AB|2=a2+b2﹣2abcos120°=a2+b2+ab，
配方得，|AB|2=（a+b）2﹣ab，
又∵ab≤（ 
）2，
∴（a+b）2﹣ab≥（a+b）2﹣ 
（a+b）2= 
（a+b）2
得到|AB|≥ 
（a+b）．
∴ 
≤ 
= 
，
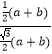即 的最大值为 ．
所以答案是： ．
练习册系列答案
名师点拨卷系列答案
英才计划期末调研系列答案
相关题目
【题目】已知学生的总成绩与数学成绩之间有线性相关关系,下表给出了5名同学在一次考试中的总成绩和数学成绩(单位:分).
学生编号 成绩 | 1 | 2 | 3 | 4 | 5 |
总成绩/x | 482 | 383 | 421 | 364 | 362 |
数学成绩/y | 78 | 65 | 71 | 64 | 61 |
(1)求数学成绩与总成绩的回归直线方程.
(2)根据以上信息,如果一个学生的总成绩为450分,试估计这个学生的数学成绩;
(3)如果另一位学生的数学成绩为92分,试估计其总成绩是多少?
