题目内容
【题目】设函数![]() 的定义域为
的定义域为![]() ,如果存在函数
,如果存在函数![]() ,使得
,使得![]() 对于一切实数
对于一切实数![]() 都成立,那么称
都成立,那么称![]() 为函数
为函数![]() 的一个承托函数.
的一个承托函数.
已知函数![]() 的图象经过点
的图象经过点![]() .
.
(![]() )若
)若![]() ,
, ![]() ,写出函数
,写出函数![]() 的一个承托函数(结论不要求注明).
的一个承托函数(结论不要求注明).
(![]() )判断是否存在常数
)判断是否存在常数![]() ,
, ![]() ,
, ![]() ,使得
,使得![]() 为函数
为函数![]() 的一个承托函数,且
的一个承托函数,且![]() 为函数
为函数![]() 的一个承托函数?若存在,求出
的一个承托函数?若存在,求出![]() ,
, ![]() ,
, ![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
【答案】(1)见解析;(2)![]() ,
, ![]() ,
, ![]() .
.
【解析】试题分析:(1)根据承托函数的定义可知, ![]() ,易得函数
,易得函数![]() ,
, ![]() 等均可;
等均可;
(2)由![]() 为函数
为函数![]() 一个承托函数,且
一个承托函数,且![]() 为函数
为函数![]() 的一个承托函数,所以
的一个承托函数,所以![]() 对
对![]() 恒成立,所以
恒成立,所以![]() ,即
,即![]() ,又
,又![]() 图象经过点
图象经过点![]() ,所以
,所以![]() ,从而将
,从而将![]() 和
和![]() 用
用![]() 表示求解恒成立即可.
表示求解恒成立即可.
试题解析:
(![]() )答案不唯一,如函数
)答案不唯一,如函数![]() ,
, ![]() 等.
等.
(![]() )因为函数
)因为函数![]() 的图象经过点
的图象经过点![]() ,
,
所以![]() .①
.①
因为![]() 为函数
为函数![]() 一个承托函数,且
一个承托函数,且![]() 为函数
为函数![]() 的一个承托函数,
的一个承托函数,
所以![]() 对
对![]() 恒成立,
恒成立,
所以![]() ,即
,即![]() ,②
,②
由①②,得![]() ,
, ![]() .
.
所以![]() .
.
由![]() 对
对![]() 恒成立,得
恒成立,得![]() 对
对![]() 恒成立.
恒成立.
当![]() 时,得
时,得![]() 对
对![]() 恒成立,显然不正确;
恒成立,显然不正确;
当![]() 时,由题意,得
时,由题意,得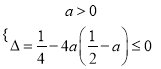 即
即![]() ,
,
所以![]() .
.
代入![]() ,得
,得![]() ,
,
化简,得![]() 对
对![]() 恒成立,符合题意.
恒成立,符合题意.
所以![]() ,
, ![]() ,
, ![]() .
.

练习册系列答案
相关题目