题目内容
【题目】已知函数![]() 是定义在
是定义在![]() 上的偶函数,且当
上的偶函数,且当![]() 时,
时, ![]() .现已画出函数
.现已画出函数![]() 在
在![]() 轴左侧的图象,如图所示,请根据图象.
轴左侧的图象,如图所示,请根据图象.
(![]() )写出函数
)写出函数![]() 的增区间.
的增区间.
(![]() )写出函数
)写出函数![]() 的解析式.
的解析式.
(![]() )若函数
)若函数![]() ,求函数
,求函数![]() 的最小值.
的最小值.

【答案】(1)见解析;(2)见解析;(3)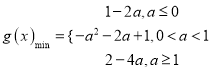
【解析】试题分析:(1)根据偶函数的图象关于![]() 轴对称,可作出
轴对称,可作出![]() 的图象,由图象可得
的图象,由图象可得![]() 的单调递增区间;
的单调递增区间;
(2)令![]() ,则
,则![]() ,根据条件可得
,根据条件可得![]() ,利用函数
,利用函数![]() 是定义在R上的偶函数,可得
是定义在R上的偶函数,可得![]() ,从而可得函数
,从而可得函数![]() 的解析式;
的解析式;
(3)先求出抛物线对称轴![]() ,然后分当
,然后分当![]() 时,当
时,当![]() 时,当
时,当![]() 时三种情况,根据二次函数的增减性解答.
时三种情况,根据二次函数的增减性解答.
试题解析:
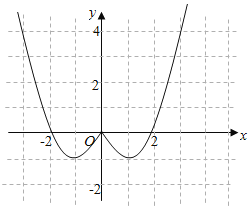 (
(![]() )函数图像如图所示,函数
)函数图像如图所示,函数![]() 的增区间:
的增区间: ![]() .
.
(![]() )当
)当![]() 时,
时, ![]() ,
, ![]() ,
,
又函数![]() 是定义在
是定义在![]() 上的偶函数,所以
上的偶函数,所以![]() .
.
所以函数![]() 的解析式为
的解析式为![]() .
.
(![]() )由(
)由(![]() )知,
)知, ![]() ,对称轴为
,对称轴为![]() .
.
①当![]() ,即
,即![]() 时,函数
时,函数![]() 的最小值为
的最小值为![]() ;
;
②当![]() ,即
,即![]() 时,函数
时,函数![]() 的最小值为
的最小值为![]() ;
;
③当![]() ,即
,即![]() 时,函数
时,函数![]() 的最小值为
的最小值为![]() ;
;
综上所述, 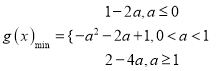 .
.

练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
【题目】某校为评估新教改对教学的影响,挑选了水平相当的两个平行班进行对比试验.甲班采用创新教法,乙班仍采用传统教法,一段时间后进行水平测试,成绩结果全部落在[60,100]区间内(满分100分),并绘制频率分布直方图如图,两个班人数均为60人,成绩80分及以上为优良. 
(1)根据以上信息填好下列2×2联表,并判断出有多大的把握认为学生成绩优良与班级有关?
是否优良 | 优良(人数) | 非优良(人数) | 合计 |
甲 | |||
乙 | |||
合计 |
(2)以班级分层抽样,抽取成绩优良的5人参加座谈,现从5人中随机选2人来作书面发言,求2人都来自甲班的概率. 下面的临界值表供参考:
P(x2k) | 0.10 | 0.05 | 0.010 |
k | 2.706 | 3.841 | 6.635 |
(以下临界值及公式仅供参考 ![]() ,n=a+b+c+d)
,n=a+b+c+d)