��Ŀ����
����Ŀ����2018��3��֣�ݵڶ���ģ�⿼���У�ijУ����100���Ŀ�ѧ���μӿ��ԣ��������Ŀ��Գɼ�����130��ռ95%�ˣ���ѧ�ɼ���Ƶ�ʷֲ�ֱ��ͼ��ͼ��
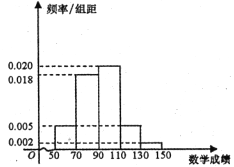
��������ɼ�������130��Ϊ�ر����㣬��100��ѧ���б��ο������ġ���ѧ�ɼ��ر�����Ĵ�Լ�������ˣ�
����������ĺ���ѧ���ƶ��ر�����Ĺ���3�ˣ�
�������ӣ����е���Щͬѧ�������ȡ2�ˣ������������Ƴɼ�������ĸ��ʣ�
�����������������ݣ����![]() ���������������Ƿ���99%�İ�����Ϊ�����ر������ͬѧ����ѧҲ�ر����㣮
���������������Ƿ���99%�İ�����Ϊ�����ر������ͬѧ����ѧҲ�ر����㣮
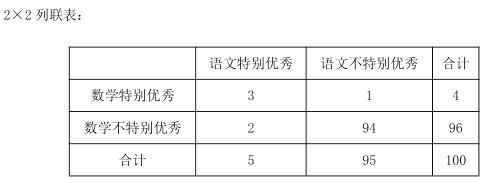
�����ر����� | ���IJ��ر����� | �ϼ� | |
��ѧ�ر����� | |||
��ѧ���ر����� | |||
�ϼ� |
![]()
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
���𰸡�������![]() ��������(i)
��������(i)![]() ����ii�����.
����ii�����.
����������������1����Ƶ�ʷֲ�ֱ��ͼ����ɼ�������130�ĸ��ʣ������õ���⣬
��2���оٳ����л����¼���
��3�����ݼ��������г��������������![]() ������ɵá�
������ɵá�
��⣺������У����100���Ŀ�ѧ���μӿ��ԣ��������Ŀ��Գɼ�����130����95%�ˣ����ijɼ��ر�����ĸ���Ϊ![]() �������ر������ͬѧ��
�������ر������ͬѧ��![]() �ˣ���ѧ�ɼ��ر�����ĸ���Ϊ
�ˣ���ѧ�ɼ��ر�����ĸ���Ϊ![]() ����ѧ�ر������ͬѧ��
����ѧ�ر������ͬѧ��![]() �ˣ�
�ˣ�
������(i)������ѧ���ƶ��������3�ˣ������������3�ˣ�
�����ƶ������3�˷ֱ�Ϊ![]() �����������3�˷ֱ�Ϊ
�����������3�˷ֱ�Ϊ![]() �����������ȡ2����������
�����������ȡ2����������![]() ��
��![]() ��
��![]()
![]()
![]() ��15�֣����������˳ɼ����������
��15�֣����������˳ɼ����������![]() 3���������������Ƴɼ�������ĸ���Ϊ��
3���������������Ƴɼ�������ĸ���Ϊ��![]() ��
��
��ii��
![]()
![]() ��95%�İ�����Ϊ�����ر������ͬѧ����ѧҲ�ر����㣮
��95%�İ�����Ϊ�����ر������ͬѧ����ѧҲ�ر����㣮

 ��ĩ1�����ʽ���������ϵ�д�
��ĩ1�����ʽ���������ϵ�д�����Ŀ���ڵ�����ͬһ�ص�۲�Զ�����ٴ�ֱ������������������10�����������������![]() ��������10��20�ֵ����DZ��
��������10��20�ֵ����DZ��![]() .�������±��жϵ�����11����ʱ���������������ӽ��ĸ�����( )
.�������±��жϵ�����11����ʱ���������������ӽ��ĸ�����( )
|
|
|
|
|
|
|
|
|
|
| 0.5 | 0.559 | 0.629 | 0.643 | 0.656 | 0.669 | 0.682 | 0.695 | 0.707 |
| 0.866 | 0.829 | 0.777 | 0.766 | 0.755 | 0.743 | 0.731 | 0.719 | 0.707 |
| 0.577 | 0.675 | 0.810 | 0.839 | 0.869 | 0.900 | 0.933 | 0.966 | 1.0 |
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
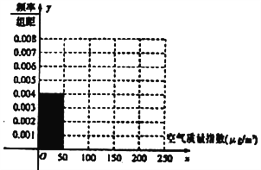
����Ŀ��ȫ����Խ��Խ��ע�����������⣬ij���վ����2018��1��ij��������![]() �����������ָ��(
�����������ָ��(![]() )������ͳ�����£�
)������ͳ�����£�
��������ָ��( |
|
|
|
|
|
���������ȼ� | ������ | ������ | �����Ⱦ | �ж���Ⱦ | �ض���Ⱦ |
���� | 20 | 40 |
| 10 | 5 |
��1����������ͳ�Ʊ���Ƶ�ʷֲ�ֱ��ͼ�е���Ϣ���![]() ��
��![]() ��ֵ�������Ƶ�ʷֲ�ֱ��ͼ��
��ֵ�������Ƶ�ʷֲ�ֱ��ͼ��
��2����Ƶ�ʷֲ�ֱ��ͼ����������ݵ���������λ����
��3���ڿ�������ָ���ֱ�����![]() ��
��![]() �ļ�������У��÷ֲ�����ķ�����ȡ
�ļ�������У��÷ֲ�����ķ�����ȡ![]() �죬�ٴ�������ѡȡ
�죬�ٴ�������ѡȡ![]() �죬���¼�
�죬���¼�![]() �����������Ϊ���������ĸ���.
�����������Ϊ���������ĸ���.