题目内容
【题目】已知函数f(x)=alnx﹣ex(a∈R).其中e是自然对数的底数.
(1)讨论函数f(x)的单调性并求极值;
(2)令函数g(x)=f(x)+ex,若x∈[1,+∞)时,g(x)≥0,求实数a的取值范围.
【答案】(1)见解析;(2)![]()
【解析】
(1)函数f(x)的定义域为(0,+∞).求出函数的导函数,然后对a分类讨论可得原函数的单调性并求得极值;
(2)对g(x)求导函数,对a分类讨论,当a≥0时,易得g(x)为单调递增,有g(x)≥g(1)=0,符合题意.当a<0时,结合零点存在定理可得存在x0∈(1,![]() )使g′(x0)=0,再结合g(1)=0,可得当x∈(1,x0)时,g(x)<0,不符合题意.由此可得实数a的取值范围.
)使g′(x0)=0,再结合g(1)=0,可得当x∈(1,x0)时,g(x)<0,不符合题意.由此可得实数a的取值范围.
(1)函数f(x)的定义域为(0,+∞).
f′(x)![]() .
.
①当a≤0时,f′(x)<0,可得函数f(x)在(0,+∞)上单调递减,f(x)无极值;
②当a>0时,由f′(x)>0得:0<x![]() ,可得函数f(x)在(0,
,可得函数f(x)在(0,![]() )上单调递增.
)上单调递增.
由f′(x)<0,得:x![]() ,可得函数f(x)在(
,可得函数f(x)在(![]() ,+∞)单调递减,
,+∞)单调递减,
∴函数f(x)在x![]() 时取极大值为:f(
时取极大值为:f(![]() )=alna﹣2a;
)=alna﹣2a;
(2)由题意有g(x)=alnx﹣ex+ex,x∈[1,+∞).
g′(x)![]() .
.
①当a≥0时,g′(x)![]() .
.
故当x∈[1,+∞)时,g(x)=alnx﹣ex+ex为单调递增函数;
g(x)≥g(1)=0,符合题意.
②当a<0时,g′(x)![]() ,令函数h(x)
,令函数h(x)![]() ,
,
由h′(x)![]() 0,c∈[1,+∞),
0,c∈[1,+∞),
可知:g′(x)![]() 为单调递增函数,
为单调递增函数,
又g′(1)=a<0,g′(x)![]() ,
,
当x![]() 时,g′(x)>0.
时,g′(x)>0.
∴存在x0∈(1,![]() )使g′(x0)=0,
)使g′(x0)=0,
因此函数g(x)在(1,x0)上单调递减,在(x0,+∞)上单调递增,
又g(1)=0,∴当x∈(1,x0)时,g(x)<0,不符合题意.
综上,所求实数a的取值范围为[0,+∞).

【题目】在2018年3月郑州第二次模拟考试中,某校共有100名文科学生参加考试,其中语文考试成绩低于130的占95%人,数学成绩的频率分布直方图如图:
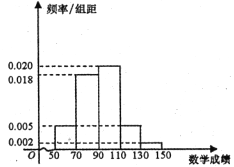
(Ⅰ)如果成绩不低于130的为特别优秀,这100名学生中本次考试语文、数学成绩特别优秀的大约各多少人?
(Ⅱ)如果语文和数学两科都特别优秀的共有3人.
(ⅰ)从(Ⅰ)中的这些同学中随机抽取2人,求这两人两科成绩都优秀的概率.
(ⅱ)根据以上数据,完成![]() 列联表,并分析是否有99%的把握认为语文特别优秀的同学,数学也特别优秀.
列联表,并分析是否有99%的把握认为语文特别优秀的同学,数学也特别优秀.
语文特别优秀 | 语文不特别优秀 | 合计 | |
数学特别优秀 | |||
数学不特别优秀 | |||
合计 |
![]()
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】近年空气质量逐步恶化,雾霾天气现象出现增多,大气污染危害加重.大气污染可引起心悸、呼吸困难等心肺疾病.为了解某市心肺疾病是否与性别有关,在某医院随机对心肺疾病入院的![]() 人进行问卷调查,得到了如下的列联表:
人进行问卷调查,得到了如下的列联表:
患心肺疾病 | 不患心肺疾病 | 合计 | |
男 |
|
|
|
女 |
|
|
|
合计 |
|
|
|
(1)用分层抽样的方法在患心肺疾病的人群中抽![]() 人,其中男性抽多少人?
人,其中男性抽多少人?
(2)在上述抽取的![]() 人中选
人中选![]() 人,求恰好有
人,求恰好有![]() 名女性的概率;
名女性的概率;
(3)为了研究心肺疾病是否与性别有关,请计算出统计量![]() ,你有多大把握认为心肺疾病与性别有关?
,你有多大把握认为心肺疾病与性别有关?
下面的临界值表供参考:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
参考公式:  ,其中
,其中![]() .
.
【题目】某商场按月订购一种家用电暖气,每销售一台获利润200元,未销售的产品返回厂家,每台亏损50元,根据往年的经验,每天的需求量与当天的最低气温有关,如果最低气温位于区间![]() ,需求量为100台;最低气温位于区间
,需求量为100台;最低气温位于区间![]() ,需求量为200台;最低气温位于区间
,需求量为200台;最低气温位于区间![]() ,需求量为300台。公司销售部为了确定11月份的订购计划,统计了前三年11月份各天的最低气温数据,得到下面的频数分布表:
,需求量为300台。公司销售部为了确定11月份的订购计划,统计了前三年11月份各天的最低气温数据,得到下面的频数分布表:
最低气温(℃) |
|
|
|
|
|
天数 | 11 | 25 | 36 | 16 | 2 |
以最低气温位于各区间的频率代替最低气温位于该区间的概率.
求11月份这种电暖气每日需求量![]() (单位:台)的分布列;
(单位:台)的分布列;
若公司销售部以每日销售利润![]() (单位:元)的数学期望为决策依据,计划11月份每日订购200台或250台,两者之中选其一,应选哪个?
(单位:元)的数学期望为决策依据,计划11月份每日订购200台或250台,两者之中选其一,应选哪个?