Question

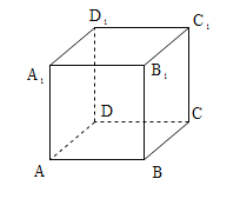
【题目】如图，正方体的棱长为1，有下列四个命题：

①与平面所成角为；

②三棱锥与三棱锥的体积比为；

③过点作平面，使得棱，，在平面上的正投影的长度相等，则这样的平面有且仅有一个；

④过作正方体的截面，设截面面积为，则的最小值为.

上述四个命题中，正确命題的序号为______.

Answer 1

【答案】①②④

【解析】

根据线面角的求解方法，棱锥体积的求解，正方体截面的相关性质，对选项进行逐一分析即可求得.

对①：连接交与，连接，作图如下：

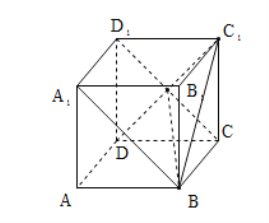
因为是正方体，故可得平面，

又因为平面，故可得，又，

故可得平面，则即为所求线面角.

在中，，

故可得，又线面角的范围为，

故，则与平面所成角为，

故①正确；

对②：因为正方体棱长为1，

故可得；

而棱锥的体积可以理解为

正方体的体积减去4个体积都和相等的三棱锥的体积，

故.

故棱锥与三棱锥的体积比为，

故②正确；

对③：若棱在平面的同侧，则为过点且与平面平行的平面；

若棱中有一条棱与另外两条棱分别在平面的异侧，则这样的平面有3个；

故满足题意的平面有4个.

故③错误；

对④：根据题意，取中点为,则过作正方体的截面如下：

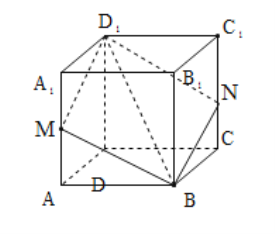
则过的所有截面中，当截面为菱形时，面积最小，

其面积为.

故④正确.

总上所述，正确的有①②④.