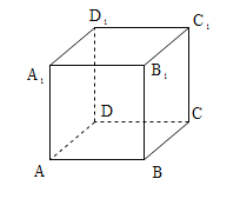
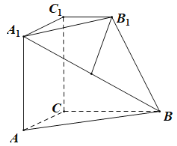
题目内容
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (其中
(其中![]() 为参数,且
为参数,且![]() ,在以
,在以![]() 为极点、
为极点、![]() 轴的非负半轴为极轴的极坐标系(两种坐标系取相同的单位长度)中,曲线
轴的非负半轴为极轴的极坐标系(两种坐标系取相同的单位长度)中,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,设直线
,设直线![]() 经过定点
经过定点![]() ,且与曲线
,且与曲线![]() 交于
交于![]() 、
、![]() 两点.
两点.
(Ⅰ)求点![]() 的直角坐标及曲线
的直角坐标及曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)求证:不论![]() 为何值时,
为何值时,![]() 为定值.
为定值.
【答案】(Ⅰ)直角坐标为![]() ,
,![]() ;(Ⅱ)见解析
;(Ⅱ)见解析
【解析】
(Ⅰ)根据题意,令直线![]() 的参数方程中
的参数方程中![]() 即可求出点
即可求出点![]() 的直角坐标,整理化简曲线
的直角坐标,整理化简曲线![]() 的极坐标方程,结合
的极坐标方程,结合![]() ,即可得到曲线
,即可得到曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)将直线![]() 的参数方程代入曲线
的参数方程代入曲线![]() 的直角坐标方程,根据参数
的直角坐标方程,根据参数![]() 的几何意义,利用韦达定理即可证明
的几何意义,利用韦达定理即可证明![]() 为定值.
为定值.
(Ⅰ)因为直线![]() 的参数方程为
的参数方程为![]() (其中
(其中![]() 为参数,且
为参数,且![]() ,
,
所以当![]() 时,得点
时,得点![]() ,即点
,即点![]() 的直角坐标为
的直角坐标为![]() ;
;
又曲线![]() 的极坐标方程为
的极坐标方程为![]() ,
,
![]() ,
,![]() ,
,
![]()
![]() ,
,![]() ,
,
即曲线![]() 的直角坐标方程为
的直角坐标方程为![]() ;
;
(Ⅱ)证明:将直线![]() 的参数方程
的参数方程![]() 代入
代入![]() ,
,
整理得![]() ,其中
,其中![]() ,
,
所以判别式△![]() ,
,
由韦达定理可得,![]() ,
,![]() ,
,
由参数方程中参数的几何意义可得,
![]() ,
,
即不论![]() 为何值时,
为何值时,![]() 都为定值1.
都为定值1.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】为了解某班学生喜爱打篮球是否与性别有关,对该班40名学生进行了问卷调查,得到了如下的![]() 列联表:
列联表:
男生 | 女生 | 总计 | |
喜爱打篮球 | 19 | 15 | 34 |
不喜爱打篮球 | 1 | 5 | 6 |
总计 | 20 | 20 | 40 |
(1)在女生的20个个体中,随机抽取2人,记随机变量![]() 为抽到“不喜爱篮球”的人数,求
为抽到“不喜爱篮球”的人数,求![]() 的分布列及数学期望
的分布列及数学期望![]() ;
;
(2)判断能否在犯错误的概率不超过0.1的条件下认为喜爱篮球与性别有关?
附: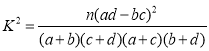 ,其中
,其中![]() .
.
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】近年来,随着国家综合国力的提升和科技的进步,截至![]() 年底,中国铁路运营里程达
年底,中国铁路运营里程达![]() 万千米,这个数字比
万千米,这个数字比![]() 年增长了
年增长了![]() 倍;高铁运营里程突破
倍;高铁运营里程突破![]() 万千米,占世界高铁运营里程的
万千米,占世界高铁运营里程的![]() 以上,居世界第一位.如表截取了
以上,居世界第一位.如表截取了![]() 年中国高铁密度的发展情况(单位:千米/万平方千米).
年中国高铁密度的发展情况(单位:千米/万平方千米).
年份 |
|
|
|
|
|
年份代码 |
|
|
|
|
|
高铁密度 |
|
|
|
|
|
已知高铁密度![]() 与年份代码
与年份代码![]() 之间满足关系式
之间满足关系式![]() (
(![]() 为大于
为大于![]() 的常数).
的常数).
(1)根据所给数据,求![]() 关于
关于![]() 的回归方程(精确到
的回归方程(精确到![]() 位);
位);
(2)利用(1)的结论,预测到哪一年,高铁密度会超过![]() 千米/万平方千米.
千米/万平方千米.
参考公式:设具有线性相关系的两个变量![]() 的一组数据为
的一组数据为![]() ,则回归方程
,则回归方程![]() 的系数:
的系数: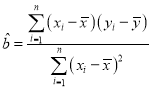 ,
,![]()
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
【题目】某土特产超市为预估2020年元旦期间游客购买土特产的情况,对2019年元旦期间的90位游客购买情况进行统计,得到如下人数分布表.
购买金额(元) |
|
|
|
|
|
|
人数 | 10 | 15 | 20 | 15 | 20 | 10 |
(1)根据以上数据完成![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为购买金额是否少于60元与性别有关.
的把握认为购买金额是否少于60元与性别有关.
不少于60元 | 少于60元 | 合计 | |
男 | 40 | ||
18 | |||
合计 |
(2)为吸引游客,该超市推出一种优惠方案,购买金额不少于60元可抽奖3次,每次中奖概率为![]() (每次抽奖互不影响,且
(每次抽奖互不影响,且![]() 的值等于人数分布表中购买金额不少于60元的频率),中奖1次减5元,中奖2次减10元,中奖3次减15元.若游客甲计划购买80元的土特产,请列出实际付款数
的值等于人数分布表中购买金额不少于60元的频率),中奖1次减5元,中奖2次减10元,中奖3次减15元.若游客甲计划购买80元的土特产,请列出实际付款数![]() (元)的分布列并求其数学期望.
(元)的分布列并求其数学期望.
附:参考公式和数据: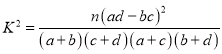 ,
,![]() .
.
附表:
| 2.072 | 2.706 | 3.841 | 6.635 | 7.879 |
| 0.150 | 0.100 | 0.050 | 0.010 | 0.005 |