题目内容
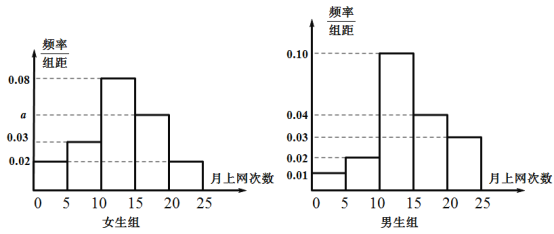
【题目】在统计调查中,问卷的设计是一门很大的学问,特别是对一些敏感性问题.例如学生在考试中有无作弊现象,社会上的偷税漏税等,更要精心设计问卷.设法消除被调查者的顾虑,使他们能够如实回答问题,否则被调查者往往会拒绝回答,或不提供真实情况.为了调查中学生中的早恋现象,随机抽出200名学生,调查中使用了两个问题.①你的血型是A型或B型(资料:我国人口![]() 型血比例41%,
型血比例41%,![]() 型血比例28%,
型血比例28%,![]() 型血比例24%.
型血比例24%.![]() 型血比例7% ).②你是否有早恋现象,让被调查者掷两枚骰子,点数之和为奇数的学生如实回答第一个问题.点数之和为偶数的学生如实回答第二个问题,回答“是”的人往一个盒子中放一个小石子,回答“否”的人什么都不放,后来在盒子中收到了57个小石子.
型血比例7% ).②你是否有早恋现象,让被调查者掷两枚骰子,点数之和为奇数的学生如实回答第一个问题.点数之和为偶数的学生如实回答第二个问题,回答“是”的人往一个盒子中放一个小石子,回答“否”的人什么都不放,后来在盒子中收到了57个小石子.
(1)试计算掷两枚骰子点数之和为偶数的机率;
(2)你能否估算出中学生早恋人数的百分比?
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)先计算抛掷两枚骰子的所有可能,再找出满足题意的可能,用古典概型的概率计算公式即可求得;
(2)根据(1)中所求,结合参考数据,先求得关于血型问题回答是的同学数量,再求出回答是早恋同学的数量,进而算出早恋比例.
(1)抛掷两枚骰子,总共有36种可能;
其中满足点数之和为偶数有以下18中可能:
![]()
![]()
故满足题意的概率![]() .
.
故掷两枚骰子点数之和为偶数的机率为![]() .
.
(2)由(1)可知,点数之和为偶函数和奇数的概率相等,
则可估算有100名同学回答第一个问题,100名同学回答第二个问题.
根据参考数据,回答第一个问题,选择是的有![]() 人;
人;
故回答第二个问题,选择是的有![]() 人.
人.
故早恋人数的占比为![]() .
.

 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案【题目】某种大型医疗检查机器生产商,对一次性购买2台机器的客户,推出两种超过质保期后两年内的延保维修优惠方案:方案一:交纳延保金7000元,在延保的两年内可免费维修2次,超过2次每次收取维修费2000元;方案二:交纳延保金10000元,在延保的两年内可免费维修4次,超过4次每次收取维修费1000元.某医院准备一次性购买2台这种机器。现需决策在购买机器时应购买哪种延保方案,为此搜集并整理了50台这种机器超过质保期后延保两年内维修的次数,得下表:
维修次数 | 0 | 1 | 2 | 3 |
台数 | 5 | 10 | 20 | 15 |
以这50台机器维修次数的频率代替1台机器维修次数发生的概率,记X表示这2台机器超过质保期后延保的两年内共需维修的次数。
(1)求X的分布列;
(2)以所需延保金及维修费用的期望值为决策依据,医院选择哪种延保方案更合算?
【题目】某公司为了对某种商品进行合理定价,需了解该商品的月销售量![]() (单位:万件)与月销售单价
(单位:万件)与月销售单价![]() (单位:元/件)之间的关系,对近
(单位:元/件)之间的关系,对近![]() 个月的月销售量
个月的月销售量![]() 和月销售单价
和月销售单价![]()
![]() 数据进行了统计分析,得到一组检测数据如表所示:
数据进行了统计分析,得到一组检测数据如表所示:
月销售单价 |
|
|
|
|
|
|
月销售量 |
|
|
|
|
|
|
(1)若用线性回归模型拟合![]() 与
与![]() 之间的关系,现有甲、乙、丙三位实习员工求得回归直线方程分别为:
之间的关系,现有甲、乙、丙三位实习员工求得回归直线方程分别为:![]() ,
,![]() 和
和![]() ,其中有且仅有一位实习员工的计算结果是正确的.请结合统计学的相关知识,判断哪位实习员工的计算结果是正确的,并说明理由;
,其中有且仅有一位实习员工的计算结果是正确的.请结合统计学的相关知识,判断哪位实习员工的计算结果是正确的,并说明理由;
(2)若用![]() 模型拟合
模型拟合![]() 与
与![]() 之间的关系,可得回归方程为
之间的关系,可得回归方程为![]() ,经计算该模型和(1)中正确的线性回归模型的相关指数
,经计算该模型和(1)中正确的线性回归模型的相关指数![]() 分别为
分别为![]() 和
和![]() ,请用
,请用![]() 说明哪个回归模型的拟合效果更好;
说明哪个回归模型的拟合效果更好;
(3)已知该商品的月销售额为![]() (单位:万元),利用(2)中的结果回答问题:当月销售单价为何值时,商品的月销售额预报值最大?(精确到
(单位:万元),利用(2)中的结果回答问题:当月销售单价为何值时,商品的月销售额预报值最大?(精确到![]() )
)
参考数据:![]() .
.
【题目】低碳经济时代,文化和旅游两大产业逐渐成为我国优先发展的“绿色朝阳产业”.为了解某市的旅游业发展情况,某研究机构对该市2019年游客的消费情况进行随机调查,得到频数分布表及频率分布直方图.
旅游消费(千元) |
|
|
|
|
频数(人) | 10 | 60 |
|
|
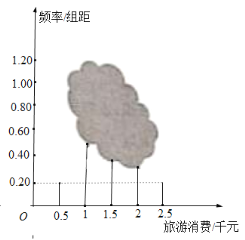
(1)由图表中数据,求![]() 的值及游客人均消费估计值(同一组中的数据以这组数据所在区间中点的值为代表)
的值及游客人均消费估计值(同一组中的数据以这组数据所在区间中点的值为代表)
(2)该机构利用最小二乘法得到2013~2017年该市的年旅游人次![]() (千万人次)与年份代码
(千万人次)与年份代码![]() 的线性回归模型:
的线性回归模型:![]() .
.
注:年份代码1~5分别对应年份2013~2017
①试求2013~2017年的年旅游人次的平均值;
②据统计,2018年该市的年旅游人次为9千万人次.建立2013~2018年该市年旅游人次![]() (千万人次)与年份代码
(千万人次)与年份代码![]() 的线性回归方程,并估计2019年该市的年旅游收入.
的线性回归方程,并估计2019年该市的年旅游收入.
注:年旅游收入=年旅游人次×人均消费
参考数据:![]() .参考公式:
.参考公式: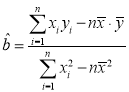 ,
,![]() .
.