题目内容
【题目】已知函数![]() ,
, ![]() .
.
(Ⅰ)求![]() 的值.
的值.
(Ⅱ)求函数![]() 在区间
在区间![]() 上的最大值和最小值,及相应的
上的最大值和最小值,及相应的![]() 的值.
的值.
(Ⅲ)求函数![]() 在区间
在区间![]() 的单调区间.
的单调区间.
【答案】(Ⅰ)![]() (Ⅱ)
(Ⅱ)![]() 时,
时, ![]()
![]() 时,
时, ![]() .(Ⅲ)
.(Ⅲ)![]() 在
在![]() 上,
上,
单调增区间![]() ,单调减区间
,单调减区间![]() .
.
【解析】试题分析:(Ⅰ)利用两角和与差的余弦公式,二倍角公式化简![]() ,则
,则![]() 即得解(Ⅱ)∵
即得解(Ⅱ)∵![]() ,
, ![]() ,结合正弦函数图像得
,结合正弦函数图像得![]() ,则及
,则及![]() 在区间
在区间![]() 上的最大值和最小值,及相应的对应
上的最大值和最小值,及相应的对应![]() 值易得解(Ⅲ)
值易得解(Ⅲ)![]() ,
,
由正弦函数图象知,当![]() 时,即
时,即![]() 时,
时, ![]() 单调递减,当
单调递减,当![]() 时,即
时,即![]() 时,
时, ![]() 单调递增,则
单调递增,则![]() 在区间
在区间![]() 的单调区间得解.
的单调区间得解.
试题解析:
(Ⅰ)∵![]()
![]() ,
,
![]() ,
,
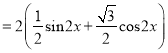 ,
,
![]() ,
,
∴![]()
![]()
![]() .
.
(Ⅱ)∵![]() ,
,
![]() ,
,
![]() ,
,
当![]() 时,
时, ![]() ,
,
此时![]() ,
,
当![]() 时,
时, ![]() ,,
,,
此时![]() .
.
(Ⅲ)∵![]() ,
,
![]() ,
,
由正弦函数图象知,
当![]() 时,
时,
即![]() 时,
时, ![]() 单调递减,
单调递减,
当![]() 时,
时,
即![]() 时,
时, ![]() 单调递增.
单调递增.
故![]() 单调减区间为
单调减区间为![]() ,
,
单调增区间为![]() .
.

 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案【题目】今有一组数据如下表:
| 1 | 2 | 3 | 4 | 5 | 6 |
| 4 | 5 | 6 | 7 | 8 | 9 |
| 90 | 84 | 83 | m | 75 | 68 |
由最小二乘法求得点![]()
![]() 的回归直线方程是
的回归直线方程是![]() ,其中
,其中![]() .
.
(Ⅰ)求m的值,并求回归直线方程;
(Ⅱ)设![]() ,我们称
,我们称![]() 为点
为点![]() 的残差,记为
的残差,记为![]() .
.
从所给的点![]()
![]() 中任取两个,求其中有且只有一个点的残差绝对值不大于1的概率.
中任取两个,求其中有且只有一个点的残差绝对值不大于1的概率.
参考公式:  .
.
【题目】某企业有甲、乙两套设备生产同一种产品,为了检测两套设备的生产质量情况,随机从两套设备生产的大量产品中各抽取了50件产品作为样本,检测一项质量指标值,若该项质量指标值落在![]() 内,则为合格品,否则为不合格品. 表1是甲套设备的样本的频数分布表,图1是乙套设备的样本的频率分布直方图.
内,则为合格品,否则为不合格品. 表1是甲套设备的样本的频数分布表,图1是乙套设备的样本的频率分布直方图.
表1:甲套设备的样本的频数分布表
质量指标值 | [95,100) | [100,105) | [105,110) | [110,115) | [115,120) | [120,125] |
频数 | 1 | 4 | 19 | 20 | 5 | 1 |
图1:乙套设备的样本的频率分布直方图

(1)填写下面列联表,并根据列联表判断是否有90%的把握认为该企业生产的这种产品的质量指标值与甲、乙两套设备的选择有关;
甲套设备 | 乙套设备 | 合计 | |||||||||||||
合格品 | |||||||||||||||
不合格品 | |||||||||||||||
合计 | ,求 |
P(K2≥k0) | 0.15 | 0.10 | 0.050 | 0.025 | 0.010 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
 .
.