题目内容
11.已知函数f(x)=ax2-6x+blnx在x=2和x=4时取得极值.(1)求a,b的值;
(2)求f(x)在x=1处的切线方程.
分析 (1)求出函数的导数,由题意可得f′(2)=0,且f′(4)=0,解方程可得a,b;
(2)求得f(x)的导数,求得切线的斜率和切点,再由点斜式方程,即可得到切线方程.
解答 解:(1)定义域为(0,+∞),f′(x)=2ax-6+$\frac{b}{x}$,
由$\left\{\begin{array}{l}{f′(2)=4a-6+\frac{b}{2}=0}\\{f′(4)=8a-6+\frac{b}{4}=0}\end{array}\right.$,
解得a=$\frac{1}{2}$,b=8,经检验a=$\frac{1}{2}$,b=8符合题意;
(2)由(1)可得f(x)=$\frac{1}{2}$x2-6x+8lnx,
f′(x)=x-6+$\frac{8}{x}$,
f(x)在x=1处的切线斜率为k=f′(1)=1-6+8=3,
切点为(1,-$\frac{11}{2}$),
则f(x)在x=1处的切线方程为y+$\frac{11}{2}$=3(x-1),
即为6x-2y-17=0.
点评 本题考查导数的运用:求切线方程和极值,主要考查导数的几何意义和极值点的意义,属于中档题.

练习册系列答案
相关题目
2.定义$\frac{n}{{p}_{1}+{p}_{2}+…+{p}_{n}}$为n个正数p1,p2,…,pn的“均倒数”.若已知正数数列{an}的前n项的“均倒数”为$\frac{1}{2n+1}$,又bn=$\frac{{a}_{n}+1}{4}$,则$\frac{1}{{b}_{1}{b}_{2}}$+$\frac{1}{{b}_{2}{b}_{3}}$+$\frac{1}{{b}_{3}{b}_{4}}$+…+$\frac{1}{{b}_{2014}{b}_{2015}}$的值为( )
| A. | $\frac{1}{2014}$ | B. | $\frac{1}{2015}$ | C. | $\frac{2013}{2014}$ | D. | $\frac{2014}{2015}$ |
6.甲、乙两歼击机的飞行员向同一架敌机射击,设击中的概率分别为0.4,0.5,则恰有一人击中敌机的概率为( )
| A. | 0.9 | B. | 0.2 | C. | 0.7 | D. | 0.5 |
16.如图是高中课程结构图:音乐所属课程是( )
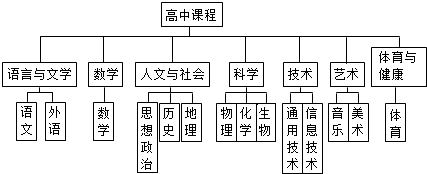

| A. | 艺术 | B. | 人文与社会 | C. | 技术 | D. | 科学 |
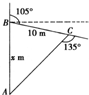 如图,在某灾区的搜救现场,一条搜救犬从A点出发沿正北方向行进x m到达B处发现生命迹象,然后向右转105°,行进10m到达C处发现另一个生命迹象,这是它向右转135°可回到出发点,那么x=$\frac{10\sqrt{6}}{3}$(单位:m).
如图,在某灾区的搜救现场,一条搜救犬从A点出发沿正北方向行进x m到达B处发现生命迹象,然后向右转105°,行进10m到达C处发现另一个生命迹象,这是它向右转135°可回到出发点,那么x=$\frac{10\sqrt{6}}{3}$(单位:m).