题目内容
6.甲、乙两歼击机的飞行员向同一架敌机射击,设击中的概率分别为0.4,0.5,则恰有一人击中敌机的概率为( )| A. | 0.9 | B. | 0.2 | C. | 0.7 | D. | 0.5 |
分析 设A为“甲命中“,B为“乙命中“,则P(A)=0.4,P(B)=0.5,由此能求出两人中恰有一人击中敌机的概率.
解答 解:设A为“甲命中“,B为“乙命中“,
则P(A)=0.4,P(B)=0.5,
∴两人中恰有一人击中敌机的概率:P=P(A$\overline{B}$+$\overline{A}$B)=P(A)P($\overline{B}$)+P($\overline{A}$)P(B)=0.4×0.5+0.6×0.5=0.5.
故选:D.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意相互独立事件同时发生的概率计算公式的求法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.设函数f(x)的导函数为f′(x),若对任意x∈R,都有f′(x)>f(x)成立,则( )
| A. | f(ln2015)<2015f(0) | |
| B. | f(ln2015)=2015f(0) | |
| C. | f(ln2015)>2015f(0) | |
| D. | f(ln2015)与2015f(0)的大小关系不确定 |
14.将函数y=$\frac{\sqrt{2}}{2}$(sinx+cosx)的图象上各点的横坐标伸长到原来的2倍,再向左平移$\frac{π}{2}$个单位,所得函数图象的解析式是( )
| A. | y=cos$\frac{x}{2}$ | B. | y=sin($\frac{x}{2}+\frac{3π}{4}$) | C. | y=-sin(2x+$\frac{π}{4}$) | D. | y=sin(2x+$\frac{3π}{4}$) |
18.执行如图所示的程序框图,如果输入的N=5,那么输出的S等于( )
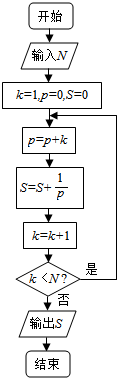

| A. | $\frac{7}{4}$ | B. | $\frac{8}{5}$ | C. | $\frac{16}{9}$ | D. | $\frac{20}{11}$ |
16.某几何体的三视图如图,则该几何体的体积为( )
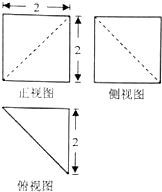

| A. | $\frac{8}{3}$ | B. | $\frac{8\sqrt{2}}{3}$ | C. | $\frac{4}{3}$ | D. | $\frac{4\sqrt{2}}{3}$ |