题目内容
20.已知函数f(x)=$\left\{\begin{array}{l}{xlnx,x>a}\\{-{x}^{2}+2x+b,x≤a}\end{array}\right.$其中a≥0,b∈R.(1)当a=0时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)当a=1,b=1时,若函数y=f(x)-c有两个零点,求实数c的取值范围;
(3)当b=-2,若对任意的x1、x2∈R,都有f(x1)<f(x2),求实数a的取值范围.
分析 (1)当a=0时,函数f(x)=$\left\{\begin{array}{l}xlnx,x>0\\-{x}^{2}+2x+b,x≤0\end{array}\right.$,利用导数法求出切点坐标和切线斜率,代入点斜式方程,可得答案;
(2)当a=1,b=1时,若函数y=f(x)-c有两个零点,则函数y=f(x)的图象与直线y=c有两个交点,利用图象法可分析出实数c的取值范围;
(3)当b=-2,若对任意的x1、x2∈R,都有f(x1)<f(x2),则函数f(x)在定义域R为增函数,在同一坐标系中画出y=xlnx,和y=-x2+2x-2的图象,数形结合可得实数a的取值范围.
解答 解:(1)当a=0时,函数f(x)=$\left\{\begin{array}{l}xlnx,x>0\\-{x}^{2}+2x+b,x≤0\end{array}\right.$,
当x>0时,f(x)=xlnx,f′(x)=lnx+1,
由f(1)=0,f′(1)=1得:切点坐标为(1,0),切线斜率为1,
故切线方程为:y=x-1;
(2)当a=1,b=1时,函数f(x)=$\left\{\begin{array}{l}xlnx,x>1\\-{x}^{2}+2x+1,x≤1\end{array}\right.$,
当x>1时,f(x)=xlnx,f′(x)=lnx+1>0,此时函数为增函数;
当x≤1时,f(x)=-x2+2x+1,f′(x)=-2x+2>0,此时函数为增函数;
故函数f(x)的图象如下图所示: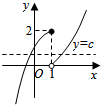
若函数y=f(x)-c有两个零点,
则函数y=f(x)的图象与直线y=c有两个交点,
则c∈(0,2],
(3)当b=-2,若对任意的x1、x2∈R,都有f(x1)<f(x2),
则函数f(x)在定义域R为增函数,
在同一坐标系中画出y=xlnx,和y=-x2+2x-2的图象如下图所示: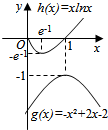 ,
,
则有a∈[$\frac{1}{e}$,1].
点评 本题考查的知识点是分段函数的应用,函数零点的判定定理,利用导数研究曲线上的某点的切线方程,是导数,函数的综合应用,难度中档.

| A. | ¬p:?x∈R,2x2+1≤0 | B. | ¬p:?x∈R,2x2+1≤0 | C. | ¬p:?x∈R,2x2+1<0 | D. | ¬p:?x∈R,2x2+1<0 |
| A. | 大前提错误 | B. | 小前提错误 | C. | 推理形式错误 | D. | 以上答案都不对 |
| A. | -$\frac{1}{2}$a2 | B. | -$\frac{3}{2}$a2 | C. | $\frac{1}{2}$a2 | D. | $\frac{3}{2}$a2 |
| A. | $\frac{1}{4}$ | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$或-$\frac{1}{2}$ | D. | $\frac{1}{2}$ |