题目内容
3．设复数z=$\frac{（2-i）^{2}+3（1+i）}{1+i}$，若az-b=2+7i（a，b∈R），求实数a，b的值．分析 先化简复数z，然后利用复数相等建立方程关系即可．
解答 解：z=$\frac{3-4i+3+3i}{1+i}$=$\frac{6-i}{1+i}$=$\frac{（6-i）（1-i）}{（1+i）（1-i）}$=$\frac{5-7i}{2}$，
∵az-b=7i，
∴$\frac{5a-7ai}{2}$-b=2+7i．
则$\left\{\begin{array}{l}{\frac{5a}{2}-b=2}\\{-\frac{7a}{2}=7}\end{array}\right.$，
解得a=-2，b=-7．
点评 本题主要考查复数的计算，根据复数相等建立方程关系是解决本题的关键．
练习册系列答案
相关题目
13．△ABC的外接圆半径为1，圆心为O，且3$\overrightarrow{OA}$+4$\overrightarrow{OB}$+5$\overrightarrow{OC}$=$\overrightarrow 0$，则$\overrightarrow{OA}•\overrightarrow{BC}$的值为（ ）
| A． | -$\frac{3}{5}$ | B． | $\frac{1}{5}$ | C． | -$\frac{6}{5}$ | D． | $\frac{3}{5}$ |
14．将函数y=$\frac{\sqrt{2}}{2}$（sinx+cosx）的图象上各点的横坐标伸长到原来的2倍，再向左平移$\frac{π}{2}$个单位，所得函数图象的解析式是（ ）
| A． | y=cos$\frac{x}{2}$ | B． | y=sin（$\frac{x}{2}+\frac{3π}{4}$） | C． | y=-sin（2x+$\frac{π}{4}$） | D． | y=sin（2x+$\frac{3π}{4}$） |
18．执行如图所示的程序框图，如果输入的N=5，那么输出的S等于（ ）
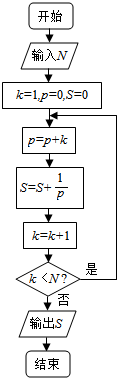
| A． | $\frac{7}{4}$ | B． | $\frac{8}{5}$ | C． | $\frac{16}{9}$ | D． | $\frac{20}{11}$ |
8．已知i为虚数单位，“因为任何数的平方都是非负数，-i是个数，所有（-i）2≥0”，这一推理中，产生错误的原因是（ ）
| A． | 大前提错误 | B． | 小前提错误 | C． | 推理形式错误 | D． | 以上答案都不对 |
12．已知菱形ABCD的边长为a，∠ABC=120°，则$\overrightarrow{BD}$•$\overrightarrow{CD}$=（ ）
| A． | -$\frac{1}{2}$a2 | B． | -$\frac{3}{2}$a2 | C． | $\frac{1}{2}$a2 | D． | $\frac{3}{2}$a2 |
13．在△ABC中，AB=2，BC=2.5，∠ABC=120°，若使△ABC绕直线BC旋转一周，则所形成的几何体的体积是（ ）
| A． | $\frac{9π}{2}$ | B． | $\frac{7π}{2}$ | C． | $\frac{5π}{2}$ | D． | $\frac{3π}{2}$ |