题目内容
19．
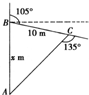如图，在某灾区的搜救现场，一条搜救犬从A点出发沿正北方向行进x m到达B处发现生命迹象，然后向右转105°，行进10m到达C处发现另一个生命迹象，这是它向右转135°可回到出发点，那么x=$\frac{10\sqrt{6}}{3}$（单位：m）．
分析 由题意设AB=x，得到各角的值，再由正弦定理可确定答案．
解答 解：由题意设AB=x可知∠ABC=180°-105°=75°，∠ACB=180°-135°=45°，∠A=60°，
根据正弦定理可得：$\frac{x}{sin∠ACB}=\frac{10}{sinA}$，即$\frac{x}{sin45°}=\frac{10}{sin60°}$，
∴x=$\frac{10\sqrt{6}}{3}$．
故答案为：$\frac{10\sqrt{6}}{3}$．
点评 本题主要考查正弦定理的应用，关键在于能够画出简图．属基础题
练习册系列答案
相关题目
9．函数y=lg（x2-2x-3）的定义域是（ ）
| A． | {x|-1＜x＜3} | B． | {x|-3＜x＜1} | C． | {x|x＜-1或x＞3} | D． | {x|x＞-3或x＞1} |
10．已知命题p：?x∈R，2x2+1＞0，则（ ）
| A． | ￢p：?x∈R，2x2+1≤0 | B． | ￢p：?x∈R，2x2+1≤0 | C． | ￢p：?x∈R，2x2+1＜0 | D． | ￢p：?x∈R，2x2+1＜0 |
7．角-2015°所在的象限为（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
14．将函数y=$\frac{\sqrt{2}}{2}$（sinx+cosx）的图象上各点的横坐标伸长到原来的2倍，再向左平移$\frac{π}{2}$个单位，所得函数图象的解析式是（ ）
| A． | y=cos$\frac{x}{2}$ | B． | y=sin（$\frac{x}{2}+\frac{3π}{4}$） | C． | y=-sin（2x+$\frac{π}{4}$） | D． | y=sin（2x+$\frac{3π}{4}$） |
4．已知函数f（x）=cos（3x+$\frac{π}{12}$），则f′（$\frac{π}{12}$）等于（ ）
| A． | $\frac{\sqrt{3}}{2}$ | B． | $\frac{3\sqrt{3}}{2}$ | C． | -$\frac{\sqrt{3}}{2}$ | D． | -$\frac{3\sqrt{3}}{2}$ |
8．已知i为虚数单位，“因为任何数的平方都是非负数，-i是个数，所有（-i）2≥0”，这一推理中，产生错误的原因是（ ）
| A． | 大前提错误 | B． | 小前提错误 | C． | 推理形式错误 | D． | 以上答案都不对 |