题目内容
8.已知椭圆C方程为$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0),左、右焦点分别是F1,F2,若椭圆C上的点$P(1,\frac{{\sqrt{3}}}{2})$到F1,F2的距离和等于4(Ⅰ)写出椭圆C的方程和焦点坐标;
(Ⅱ)直线l过定点M(0,2),且与椭圆C交于不同的两点A,B,
(i)若直线l倾斜角为$\frac{π}{3}$,求|AB|的值.
(ii)若$\overrightarrow{OA}•\overrightarrow{OB}$>0,求直线l的斜率k的取值范围.
分析 (Ⅰ)通过椭圆定义及将点$P(1,\frac{{\sqrt{3}}}{2})$代入椭圆C,计算即得结论;
(Ⅱ)(i)通过设A(x1,y1),B(x2,y2),将直线l的方程代入椭圆C的方程,利用韦达定理计算即可;(ii)通过设l:y=kx+2并代入椭圆C的方程,利用根的判别式大于0可得k2>$\frac{3}{4}$,利用韦达定理及$\overrightarrow{OA}•\overrightarrow{OB}$>0计算可得k2<4,进而可得结论.
解答 解:(Ⅰ)由题意得:2a=4,即a=2,
又点$P(1,\frac{{\sqrt{3}}}{2})$在椭圆C上,∴$\frac{1}{4}+\frac{\frac{3}{4}}{{b}^{2}}=1$,即b2=1,
∴椭圆C的方程为:$\frac{{x}^{2}}{4}+{y}^{2}=1$,
焦点F1(-$\sqrt{3}$,0),F2($\sqrt{3}$,0);
(Ⅱ)(i)设A(x1,y1),B(x2,y2),
直线l的斜率为$\sqrt{3}$,且过点M(0,2),
故直线l的方程为:y=$\sqrt{3}$x+2,代入椭圆C的方程,
整理得:13x2+16$\sqrt{3}$x+12=0,
由韦达定理可知:x1+x2=-$\frac{16\sqrt{3}}{13}$,x1x2=$\frac{12}{13}$,
∴|AB|=$\sqrt{1+{k}^{2}}$|x1-x2|=2$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\frac{24}{13}$;
(ii)由题意得直线l的斜率存在且不为0,
设l:y=kx+2,代入椭圆C的方程,整理得:
(1+4k2)x2+16kx+12=0,
∵△=(16k)2-4•(1+4k2)•12=16(4k2-3)>0,
∴k2>$\frac{3}{4}$,
设A(x1,y1),B(x2,y2),
由韦达定理可知:x1+x2=-$\frac{16k}{1+4{k}^{2}}$,x1x2=$\frac{12}{1+4{k}^{2}}$,
$\overrightarrow{OA}•\overrightarrow{OB}$=x1x2+y1y2>0,
又y1y2=(kx1+2)•(kx2+2)=k2x1x2+2k(x1+x2)+4,
∴x1x2+y1y2=(1+k2)x1x2+2k(x1+x2)+4
=(1+k2)$\frac{12}{1+4{k}^{2}}$+2k(-$\frac{16k}{1+4{k}^{2}}$)+4
=$\frac{4(4-{k}^{2})}{1+4{k}^{2}}$>0,
∴k2<4,
∴$\frac{3}{4}$<k2<4,
∴直线l的斜率k的取值范围是:(-2,-$\frac{\sqrt{3}}{2}$)∪($\frac{\sqrt{3}}{2}$,2).
点评 本题是一道直线与圆锥曲线的综合题,考查运算求解能力,注意解题方法的积累,属于中档题.

 阅读快车系列答案
阅读快车系列答案 某高校在2009年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组,得到的频率分布表如图所示.
某高校在2009年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组,得到的频率分布表如图所示.(1)请先求出频率分布表中①、②位置相应数据,再在答题纸上完成下列频率分布直方图;
(2)为了能选拔出最优秀的学生,高校决定在笔试成绩高的第3、4、5组中用分层抽样抽取6名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试?
(3)在(2)的前提下,学校决定在6名学生中随机抽取2名学生接受A考官进行面试,求:第4组至少有一名学生被考官A面试的概率?
| 组号 | 分组 | 频数 | 频率 |
| 第1组 | [160,165) | 5 | 0.050 |
| 第2组 | [165,170) | ① | 0.350 |
| 第3组 | [170,175) | 30 | ② |
| 第4组 | [175,180) | 20 | 0.200 |
| 第5组 | [180,185) | 10 | 0.100 |
| 合计 | 100 | 1.00 | |
| A. | 双曲线$\frac{{x}^{2}}{25}$-$\frac{{y}^{2}}{9}$=1与椭圆$\frac{{x}^{2}}{35}$+y2=1有相同的焦点 | |
| B. | “0<x<2”是“x2-2x-3<0”充分不必要条件 | |
| C. | “若xy=0,则x、y中至少有一个为0”的否命题是真命题. | |
| D. | “?x∈R,使x2-2x+3≤0” |
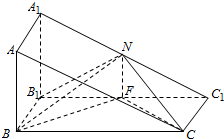 直三棱柱ABC-A1B1C1中,AB=BB1=$\frac{1}{2}$BC,∠ABC=90°,N、F分别是A1C1、B1C1的中点.
直三棱柱ABC-A1B1C1中,AB=BB1=$\frac{1}{2}$BC,∠ABC=90°,N、F分别是A1C1、B1C1的中点.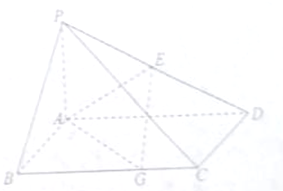 如图,在四棱锥P-ABCD中,底圆ABCD是矩形,PA⊥平面ABCD,PA=AB=2,BC=4,E是PD的中点,点G在线段BC上,且BG=3.
如图,在四棱锥P-ABCD中,底圆ABCD是矩形,PA⊥平面ABCD,PA=AB=2,BC=4,E是PD的中点,点G在线段BC上,且BG=3.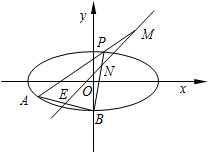 如图,已知椭圆$C:\frac{x^2}{12}+\frac{y^2}{4}=1$,点B是其下顶点,过点B的直线交椭圆C于另一点A(A点在x轴下方),且线段AB的中点E在直线y=x上.
如图,已知椭圆$C:\frac{x^2}{12}+\frac{y^2}{4}=1$,点B是其下顶点,过点B的直线交椭圆C于另一点A(A点在x轴下方),且线段AB的中点E在直线y=x上.