题目内容
17.已知实数x,y满足x2+(y-1)2=1,则$\frac{y+2}{x+1}$的最值的情况是[$\frac{4}{3}$,+∞).分析 由题意,借助已知动点在圆上任意动,而所求式子形式可以联想成在单位圆上动点P与定点A构成的斜率,进而求解
解答 解:由题意作出如下图形: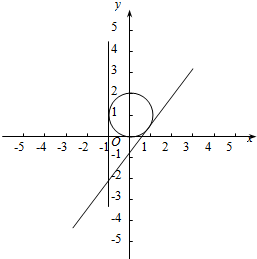
令k=$\frac{y+2}{x+1}$,则k可看作圆x2+(y-1)2=1上的动点P到定点A(-1,-2)的连线的斜率而相切时的斜率,
由于此时直线与圆相切,设直线方程为:y+2=k(x+1),
化为直线一般式为:kx-y+k-2=0,
利用直线与圆相切建立关于k的方程为:$\frac{|-1+k-2|}{\sqrt{1+{k}^{2}}}$=1,
∴k=$\frac{4}{3}$,
而由题意及点P所在的位置图可以知道斜率k的最小值为$\frac{4}{3}$,
而由于点A的横坐标为-1时,此时过点A与单位圆相切的直线的倾斜角为90°,所以斜率无最大值.
综合可得,$\frac{y+2}{x+1}$的取值范围是[$\frac{4}{3}$,+∞).
故答案为:[$\frac{4}{3}$,+∞).
点评 此题重点考查了已知两点坐标写斜率,及直线与圆的相切与相交的关系,还考查了利用几何思想解决代数式子的等价转化的思想

练习册系列答案
相关题目