题目内容
6.已知直线AB的倾斜角为45°,椭圆$\frac{{x}^{2}}{6}+\frac{{y}^{2}}{3}$=1上存在关于直线AB对称的两点.则直线AB在y轴上的截距的取值范围是(-1,1).分析 通过设M(x1,y1)、N(x2,y2),设直线MN的方程为y=-x+b并与椭圆方程联立,利用韦达定理及根的判别式大于零、MN的中点T(x0,y0)在直线y=x+m上计算即得结论.
解答 解:设椭圆$\frac{{x}^{2}}{6}+\frac{{y}^{2}}{3}$=1上存在关于直线y=x+m对称的两点为M(x1,y1)、N(x2,y2),
根据对称性可知线段MN被直线y=x+m垂直平分,且MN的中点T(x0,y0)在直线y=x+m上,且kMN=-1,
故可设直线MN的方程为y=-x+b,
联立直线MN与椭圆方程,整理可得:3x2-4bx+2b2-6=0,
∴x1+x2=$\frac{4b}{3}$,y1+y2=2b-(x1+x2)=2b-$\frac{4b}{3}$=$\frac{2b}{3}$,
由△=16b2-24(b2-3)>0,可得-3<b<3,
∴x0=$\frac{{x}_{1}+{x}_{2}}{2}$=$\frac{2b}{3}$,y0=$\frac{{y}_{1}+{y}_{2}}{2}$=$\frac{b}{3}$,
∵MN的中点T(x0,y0)在直线y=x+m上,
∴$\frac{2b}{3}$+m=$\frac{b}{3}$,m=-$\frac{b}{3}$,
∴-1<m<1,
故答案为:(-1,1).
点评 本题主要考查了直线与椭圆的位置关系的应用,解题的关键是灵活应用已知中的对称性设出直线方程,且由中点在直线上建立m、b之间的关系,还要注意方程的根与系数的关系的应用,注意解题方法的积累,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.a、b为任意实数,若(a,b)在曲线f(x,y)=0上,且(b,a)也在曲线f(x,y)=0上,则曲线f(x,y)=0的几何特征是( )
| A. | 关于x轴对称 | B. | 关于y轴对称 | C. | 关于原点对称 | D. | 关于直线y=x对称 |
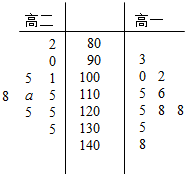 高三学生小周把自己在高二时的10次数学考试成绩和高三时的10次数学考试成绩(试卷总分150分)进行统计,统计数据用茎叶图表示(如图所示)
高三学生小周把自己在高二时的10次数学考试成绩和高三时的10次数学考试成绩(试卷总分150分)进行统计,统计数据用茎叶图表示(如图所示)