题目内容
9．定义运算“*”如下，x*y=$\left\{\begin{array}{l}{x，x≥y}\\{y，x＜y}\\{\;}\end{array}\right.$，若函数f（x）=m-（1-2x）*（2x-2）有两个零点，则m的取值范围是（-$\frac{1}{2}$，1）．分析 若函数f（x）=m-（1-2x）*（2x-2）有两个零点，则函数y=（1-2x）*（2x-2）的图象与直线y=m有两个交点，数形结合可得答案．
解答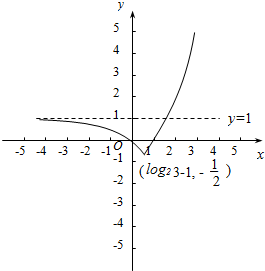 
解：若函数f（x）=m-（1-2x）*（2x-2）有两个零点，
则函数y=（1-2x）*（2x-2）的图象与直线y=m有两个交点，
函数y=（1-2x）*（2x-2）=$\left\{\begin{array}{l}1-{2}^{x}，x≤{log}_{2}3-1\\{2}^{x}-2，x＞{log}_{2}3-1\end{array}\right.$的图象如下图所示：
由图可得：m∈（-$\frac{1}{2}$，1），
故答案为：（-$\frac{1}{2}$，1）
点评 本题考查的知识点是分段函数的应用，函数的零点，难度中档．
练习册系列答案
相关题目
19．如图，在三角形ABC中，已知AB=2，AC=3，∠BAC=θ，点D为BC的三等分点．则$\overrightarrow{AD}•\overrightarrow{BC}$的取值范围为（ ）
| A． | $（{-\frac{11}{3}，\frac{13}{3}}）$ | B． | $（{\frac{1}{3}，\;\frac{7}{3}}）$ | C． | $（{-\frac{5}{3}，\frac{55}{3}}）$ | D． | $（{-\frac{5}{3}，\;\frac{7}{3}}）$ |
14．a、b为任意实数，若（a，b）在曲线f（x，y）=0上，且（b，a）也在曲线f（x，y）=0上，则曲线f（x，y）=0的几何特征是（ ）
| A． | 关于x轴对称 | B． | 关于y轴对称 | C． | 关于原点对称 | D． | 关于直线y=x对称 |