题目内容

7．已知等比数列{an}是递增数列，Sn是前n项和，若a1，a3是方程x2-5x+4=0的两个根，则公比q=2，S6=31．

分析 由a1，a3是方程x2-5x+4=0的两个根，解得a1，a3．利用等比数列的通项公式、前n项和公式即可得出．

解答 解：等比数列{an}是递增数列，∴a1＜a3．
∵a1，a3是方程x2-5x+4=0的两个根，
解得a1=1，a3=4．
∴4=q2，q＞1，
解得q=2．
∴S6=$\frac{{2}^{6}-1}{2-1}$=31．
故答案分别为：2；31．

点评 本题考查了等差数列的通项公式、前n项和公式，考查了推理能力与计算能力，属于中档题．

练习册系列答案
相关题目
17．已知实数x，y满足x2+（y-1）2=1，则$\frac{y+2}{x+1}$的最值的情况是[$\frac{4}{3}$，+∞）．
18．函数y=x2+x在区间[1，2]上的平均变化率为4．
15．已知函数y=loga（x+3）（a＞0，a≠1）的图象过定点A，若点A也在函数f（x）=3x+b的图象上，则f（log32）=$\frac{17}{9}$．
2．已知f（x）=$\left\{\begin{array}{l}{（3a-1）x+4a，x＜1}\\{-{x}^{2}+ax-1，x≥1}\end{array}\right.$是（-∞，+∞）上的减函数，求实数a的取值范围．
12．已知等差数列{an}满足a3=7，a5+a7=26，则通项公式an=（　　）
A．2n-1B．2n+1C．3n+1D．4n+1
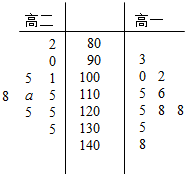19．（1）已知命题p：（x+2）（x-10）≤0，命题q：1-m≤x≤1+m，m＞0，若?q是?p的必要不充分条件，求实数m的取值范围．
（2）已知命题p：关于x的不等式x2+2ax+4＞0对一切x∈R恒成立，命题q：函数f（x）=（3-2a）x是增函数，若p∨q为真，p∧q为假，求实数a的取值范围．
16．高三学生小周把自己在高二时的10次数学考试成绩和高三时的10次数学考试成绩（试卷总分150分）进行统计，统计数据用茎叶图表示（如图所示）
（1）求小周在高三的10次数学考试成绩的中位数：
（2）若茎叶阳中高二成绩栏内的数据恰有两个众数．
（Ⅰ）求茎叶图中a的值：
（Ⅱ）随机抽取茎叶图中的一个高二成绩，其分值高于高三成绩平均分的概率是多少？
17．在△ABC中，角A，B，C所对的边分别为a，b，c，已知cos2A+cos2B=2cos2C，那么cosC的最小值为$\frac{1}{2}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网