题目内容
18.函数y=sin3x的图象可以由函数y=cos3x的图象向左平移a个单位得到的,则a的最小值为-$\frac{π}{6}$.分析 由函数y=Asin(ωx+φ)的图象变换可得cos[3(x+a)]=cos(3x+3a)=sin3x=cos(3x+$\frac{3π}{2}$)=cos(3x-$\frac{π}{2}$),从而得解.
解答 解:由于函数y=cos[3(x+a)]=cos(3x+3a)=sin3x=cos(3x+$\frac{3π}{2}$)=cos(3x-$\frac{π}{2}$),
故3x+3a=3x-$\frac{π}{2}$,解得:a=-$\frac{π}{6}$.
故答案为:-$\frac{π}{6}$.
点评 本题主要考查了诱导公式,函数y=Asin(ωx+φ)的图象变换规律的应用,属于基本知识的考查.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.双曲线$\frac{x^2}{10}-\frac{y^2}{2}$=1的焦距为( )
| A. | 2$\sqrt{3}$ | B. | 4$\sqrt{2}$ | C. | 2$\sqrt{2}$ | D. | 4$\sqrt{3}$ |
10.长方体的一个顶点上三条棱长分别为2,4,5,则它的表面积为( )
| A. | 22 | B. | 40 | C. | 45 | D. | 76 |
12.若不等式x2-logax<0对任意的x∈(0,$\frac{1}{2}$)恒成立,则实数a的取值范围是( )
| A. | (0,1) | B. | [$\frac{1}{16}$,1) | C. | (1,+∞) | D. | (0,$\frac{1}{16}$] |
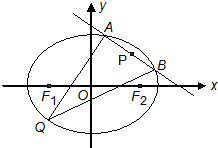 如图所示,已知椭圆C的方程为$\frac{x^2}{2}+{y^2}$=1,F1,F2分别是椭圆C的左、右焦点,直线AB:y=kx+m(k<0)与椭圆C交于不同的A,B两点.
如图所示,已知椭圆C的方程为$\frac{x^2}{2}+{y^2}$=1,F1,F2分别是椭圆C的左、右焦点,直线AB:y=kx+m(k<0)与椭圆C交于不同的A,B两点.