题目内容
【题目】在直角坐标系xoy中,曲线C1: ![]() (t为参数,t≠0),其中0≤α<π,在以O为极点,x轴正半轴为极轴的极坐标系中,曲线C2:ρ=2sinθ,曲线C3:ρ=2
(t为参数,t≠0),其中0≤α<π,在以O为极点,x轴正半轴为极轴的极坐标系中,曲线C2:ρ=2sinθ,曲线C3:ρ=2 ![]() cosθ. (Ⅰ)求C2与C3交点的直角坐标;
cosθ. (Ⅰ)求C2与C3交点的直角坐标;
(Ⅱ)若C2与C1相交于点A,C3与C1相交于点B,求|AB|的最大值.
【答案】解:(Ⅰ)曲线C2:ρ=2sinθ得ρ2=2ρsinθ,即x2+y2=2y,①
C3:ρ=2 ![]() cosθ,则ρ2=2
cosθ,则ρ2=2 ![]() ρcosθ,即x2+y2=2
ρcosθ,即x2+y2=2 ![]() x,②
x,②
由①②得 ![]() 或
或 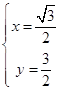 ,
,
即C2与C3交点的直角坐标为(0,0),( ![]() ,
, ![]() );
);
(Ⅱ)曲线C1的直角坐标方程为y=tanαx,
则极坐标方程为θ=α(ρ∈R,ρ≠0),其中0≤a<π.
因此A得到极坐标为(2sinα,α),B的极坐标为(2 ![]() cosα,α).
cosα,α).
所以|AB|=|2sinα﹣2 ![]() cosα|=4|sin(α
cosα|=4|sin(α ![]() )|,
)|,
当α= ![]() 时,|AB|取得最大值,最大值为4.
时,|AB|取得最大值,最大值为4.
【解析】(Ⅰ)将C2与C3转化为直角坐标方程,解方程组即可求出交点坐标;(Ⅱ)求出A,B的极坐标,利用距离公式进行求解.

【题目】微信红包是一款可以实现收发红包、查收记录和提现的手机应用.某网络运营商对甲、乙两个品牌各5种型号的手机在相同环境下,对它们抢到的红包个数进行统计,得到如表数据:
型号 | Ⅰ | Ⅱ | Ⅲ | Ⅳ | Ⅴ |
甲品牌(个) | 4 | 3 | 8 | 6 | 12 |
乙品牌(个) | 5 | 7 | 9 | 4 | 3 |
(Ⅰ)如果抢到红包个数超过5个的手机型号为“优”,否则“非优”,请据此判断是否有85%的把握认为抢到的红包个数与手机品牌有关?
(Ⅱ)如果不考虑其它因素,要从甲品牌的5种型号中选出3种型号的手机进行大规模宣传销售.
①求在型号Ⅰ被选中的条件下,型号Ⅱ也被选中的概率;
②以X表示选中的手机型号中抢到的红包超过5个的型号种数,求随机变量X的分布列及数学期望E(X).
下面临界值表供参考:
P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式:K2= ![]() .
.
【题目】随着网络的发展,人们可以在网络上购物、玩游戏、聊天、导航等,所以人们对上网流量的需求越来越大.某电信运营商推出一款新的“流量包”套餐.为了调查不同年龄的人是否愿意选择此款“流量包”套餐,随机抽取50个用户,按年龄分组进行访谈,统计结果如表.
组号 | 年龄 | 访谈人数 | 愿意使用 |
1 | [18,28) | 4 | 4 |
2 | [28,38) | 9 | 9 |
3 | [38,48) | 16 | 15 |
4 | [48,58) | 15 | 12 |
5 | [58,68) | 6 | 2 |
(Ⅰ)若在第2、3、4组愿意选择此款“流量包”套餐的人中,用分层抽样的方法抽取12人,则各组应分别抽取多少人?
(Ⅱ)若从第5组的被调查者访谈人中随机选取2人进行追踪调查,求2人中至少有1人愿意选择此款“流量包”套餐的概率.
(Ⅲ)按以上统计数据填写下面2×2列联表,并判断以48岁为分界点,能否在犯错误不超过1%的前提下认为,是否愿意选择此款“流量包”套餐与人的年龄有关?
年龄不低于48岁的人数 | 年龄低于48岁的人数 | 合计 | |
愿意使用的人数 | |||
不愿意使用的人数 | |||
合计 |
参考公式: ![]() ,其中:n=a+b+c+d.
,其中:n=a+b+c+d.
P(k2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |