Question

【题目】如图，在三棱柱中，平面，分别为的中点，且．

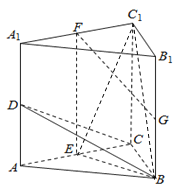
（1）证明：；

（2）证明：直线与平面相交；

（3）求直线与平面所成角的正弦值.

Answer 1

【答案】（1）见解析；（2）

【解析】

（1）由线面垂直的性质可得，由等腰三角形的性质可得，由线面垂直的判断定理可得出平面，从而可得结果；（2）设，则，又，可得四边形是梯形，则直线与直线相交，可得与平面BCD相交；（3）先证明平面 从而就是所求的角求得.

（1）在三棱柱ABC-A1B1C1中，∵CC1⊥平面ABC，∴四边形A1ACC1为矩形．

又E，F分别为AC，A1C1的中点，∴AC⊥ EF．

∵AB=BC．∴AC⊥BE，∴AC⊥ 平面BEF．

又G是BB1中点，BB1 //EF，∴G在平面BEF内，∴ AC⊥FG

（2）设，则，又，所以，四边形是梯形，所以，直线与直线相交，可得与平面BCD相交，

（3）过作于点，连，

易证平面，∴ ，

∴ 平面 从而就是所求的角

计算得，