Question

【题目】已知函数f（x）= ，若存在实数x1 ， x2 ， x3 ， x4满足f（xl）=f（x2）=f（x3）=f（x4），且x1＜x2＜x3＜x4 ， 则x1x2x3x4的取值范围是

Answer 1

【答案】（27， ）
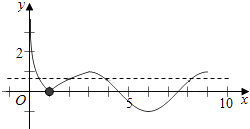
【解析】解：解：画出函数f（x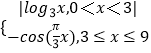）= 的图象，
令f（xl）=f（x2）=f（x3）=f（x4）=a，
作出直线y=a，
由x=3时，f（3）=﹣cosπ=1；x=9时，f（9）=﹣cos3π=1．
由图象可得，当0＜a＜1时，直线和曲线y=f（x）有四个交点．
由图象可得0＜x1＜1＜x2＜3＜x3＜4.5，7.5＜x4＜9，
则|log3x1|=|log3x2|，即为﹣log3x1=log3x2 ， 可得x1x2=1，
由y=﹣cos（ x）的图象关于直线x=6对称，可得x3+x4=12，
则x1x2x3x4=x3（12﹣x3）=﹣（x3﹣6）2+36在（3，4.5）递增，
即有x1x2x3x4∈（27， ）．
所以答案是：（27， ）．