题目内容
【题目】要在墙上开一个上部为半圆，下部为矩形的窗户（如图所示），在窗框总长度为l的条件下，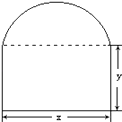 
（1）请写出窗户的面积S与圆的直径x的函数关系；
（2）要使窗户透光面积最大，窗户应具有怎样的尺寸？并写出最大值．
【答案】
（1）解：设半圆的直径为x，矩形的高度为y，
窗户透光面积为S，
则窗框总长l= 
+x+2y
∴y= 
S= 
= 
+ x
∴S=﹣ 
x2+ 
（0＜x＜ 
）
（2）解：S=﹣ （x﹣ 
）2+ 
当x= 时，Smax=
此时，y= 
= 
答：窗户中的矩形高为 ，且半径等于矩形的高时，窗户的透光面积最大
【解析】（1）窗户的面积S由两部分组成，一部分是半圆，一部分是矩形，分别求出它们的面积，相加即可得到窗户的面积S与圆的直径x的函数关系；（2）根据二次函数的性质可求出面积关于直径x的函数的最值，然后求出取最值时相应的x即可．
练习册系列答案
相关题目
