题目内容
【题目】已知函数f（x）=log4（ax2﹣4x+a）（a∈R），若f（x）的值域为R，则实数a的取值范围是（ ）
A.[0，2]
B.（2，+∞）
C.（0，2]
D.（﹣2，2）
【答案】A
【解析】解：函数f（x）=log4（ax2﹣4x+a）（a∈R），
f（x）的值域为R，
只需保证函数y=ax2﹣4x+a的值域能取到大于等于0的数．
当a=0时，函数y值域能取到大于等于0的数，
当a≠0时，要使函数y值域能取到大于等于0的数，
则需满足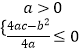 
，解得：0＜a≤2．
综上所得：实数a的取值范围是[0，2]．
故选A．
【考点精析】利用函数的值域对题目进行判断即可得到答案，需要熟知求函数值域的方法和求函数最值的常用方法基本上是相同的．事实上，如果在函数的值域中存在一个最小（大）数，这个数就是函数的最小（大）值．因此求函数的最值与值域，其实质是相同的．
练习册系列答案
名校课堂系列答案
相关题目
【题目】某企业人力资源部为了研究企业员工工作积极性和对待企业改革态度的关系，随机抽取了72名员工进行调查，所得的数据如表所示：
积极支持改革 | 不太支持改革 | 合 计 | |
工作积极 | 28 | 8 | 36 |
工作一般 | 16 | 20 | 36 |
合 计 | 44 | 28 | 72 |
对于人力资源部的研究项目，根据上述数据能得出的结论是
（参考公式与数据： 
．当Χ2＞3.841时，有95%的把握说事件A与B有关；当Χ2＞6.635时，有99%的把握说事件A与B有关； 当Χ2＜3.841时认为事件A与B无关．）（ ）
A.有99%的把握说事件A与B有关
B.有95%的把握说事件A与B有关
C.有90%的把握说事件A与B有关
D.事件A与B无关
