Question

【题目】直线1通过点P（1，3）且与两坐标轴的正半轴交于A、B两点．
（1）直线1与两坐标轴所围成的三角形面积为6，求直线1的方程；
（2）求OA+OB的最小值；
（3）求PAPB的最小值．

Answer 1

【答案】
（1）解：设直线l的方程为y﹣3=k（x﹣1）（k＜0），

由x=0，得y=3﹣k，由y=0，得x= ，

∴ =6，解得：k=﹣3

（2）解：OA+OB=3﹣k+1﹣ =4+（﹣k）+（﹣ ） ．

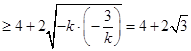当且仅当﹣k=﹣ ，即k=﹣ 时上式“=”成立

（3）解：设直线l的倾斜角为α，则它的方程为 （t为参数），

由A、B是坐标轴上的点，不妨设yA=0，xB=0，

∴0=3+tsinα，即PA=|t|= ，

0=3+tcosα，即PB=|t|=﹣ ．

故PAPB= =﹣ ．∵90°＜α＜180°，

∴当2α=270°，即α=135°时，PAPB有最小值．

∴直线方程为 （t为参数），化为普通方程即x+y﹣4=0

【解析】（1）设出直线l的方程为y﹣3=k（x﹣1）（k＜0），求出直线在两坐标轴上的截距，代入三角形面积公式得答案；（2）写出OA+OB的含有k的代数式，利用基本不等式求得最值；（3）设出直线l的参数方程，利用t的几何意义求出PA，PB然后利用三角函数求最值．
【考点精析】关于本题考查的截距式方程，需要了解直线的截距式方程：已知直线与轴的交点为A，与轴的交点为B，其中才能得出正确答案．