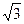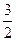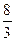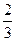题目内容
设F1、F2是椭圆 +
+ =1的两个焦点,P是椭圆上一点,且|PF1|-|PF2|=1,则cos∠F1PF2=___________.
=1的两个焦点,P是椭圆上一点,且|PF1|-|PF2|=1,则cos∠F1PF2=___________.
 +
+ =1的两个焦点,P是椭圆上一点,且|PF1|-|PF2|=1,则cos∠F1PF2=___________.
=1的两个焦点,P是椭圆上一点,且|PF1|-|PF2|=1,则cos∠F1PF2=___________.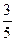
由椭圆定义|PF1|+|PF2|=2a=2×2=4,又|PF1|-|PF2|=1,
联立解得|PF1|=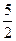 ,|PF2|=
,|PF2|=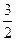 .
.
又F1F2=2c=2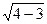 =2,
=2,
在△PF1F2中,由余弦定理得
cos∠F1PF2=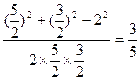 .
.
联立解得|PF1|=
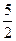 ,|PF2|=
,|PF2|=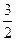 .
.又F1F2=2c=2
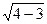 =2,
=2,在△PF1F2中,由余弦定理得
cos∠F1PF2=
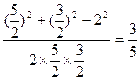 .
.
练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
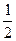 ,tan∠MNP=-2,适当建立坐标系,求以M、N为焦点,且过点P的椭圆方程.
,tan∠MNP=-2,适当建立坐标系,求以M、N为焦点,且过点P的椭圆方程.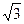 ,且和直线3x+2
,且和直线3x+2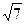 y-16=0相切,求椭圆方程.
y-16=0相切,求椭圆方程.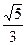 ,一条准线为y=3.
,一条准线为y=3. ,求∠ABF.
,求∠ABF.
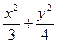 ="1"
="1"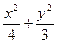 =1
=1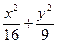 ="1"
="1"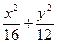 =1
=1 的椭圆的一个焦点是(0,4),则此椭圆的准线方程为__________.
的椭圆的一个焦点是(0,4),则此椭圆的准线方程为__________.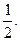 点
点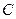 在
在 轴上,
轴上,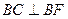 ,且
,且 、
、 三点确定的圆
三点确定的圆 恰好与直线
恰好与直线 相切.
相切. 交椭圆于
交椭圆于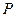 、
、 两点,在
两点,在 ,使得
,使得 恰好为△
恰好为△ 的内角平分线,若存在,求出点
的内角平分线,若存在,求出点
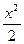 +
+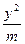 =1的离心率
=1的离心率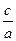 为
为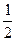 ,则m等于( )
,则m等于( )