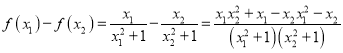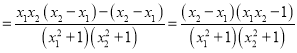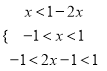题目内容
【题目】已知函数f(x)=x2eax .
(Ⅰ)当a<0时,讨论函数f(x)的单调性;
(Ⅱ)在(1)条件下,求函数f(x)在区间[0,1]上的最大值;
(Ⅲ)设函数g(x)=2ex﹣ ![]() ,求证:当a=1,对x∈(0,1),g(x)﹣xf(x)>2恒成立.
,求证:当a=1,对x∈(0,1),g(x)﹣xf(x)>2恒成立.
【答案】解:(Ⅰ)f'(x)=eax(ax2+2x),令f'(x)=0可得,x=0或 ![]() . 又a<0,则可知f(x)在(﹣∞,0)和
. 又a<0,则可知f(x)在(﹣∞,0)和 ![]() 上单调递减;在
上单调递减;在 ![]() 上单调递增.
上单调递增.
(Ⅱ)在(Ⅰ)条件下,当 ![]() ,即﹣2≤a<0时,f(x)在[0,1]上单调递增,
,即﹣2≤a<0时,f(x)在[0,1]上单调递增,
则f(x)最大值为f(1)=ea;
当 ![]() ,即a<﹣2时,f(x)在
,即a<﹣2时,f(x)在 ![]() 单调递增,在
单调递增,在 ![]() 上单调递减,
上单调递减,
则f(x)的最大值为 ![]() .
.
(Ⅲ)要证g(x)﹣xf(x)>2,即证 ![]() ,
,
令h(x)=(2﹣x3)ex , 则h'(x)=(﹣x3﹣3x2+2)ex=﹣ex(x+1)(x2+2x﹣2),
又x∈(0,1),可知在x∈(0,1)内存在极大值点,又h(0)=2,h(1)=e,
则h(x)在x∈(0,1)上恒大于2,(11分)
而 ![]() 在x∈(0,1)上恒小于2,因此g(x)﹣xf(x)>2在x∈(0,1)上恒成立
在x∈(0,1)上恒小于2,因此g(x)﹣xf(x)>2在x∈(0,1)上恒成立
【解析】(Ⅰ)求出函数的导数,根据a的符号,求出函数的单调区间即可;(Ⅱ)通过讨论a的范围,得到函数的单调区间,求出函数的最值即可;(Ⅲ)问题转化为证明 ![]() ,令h(x)=(2﹣x3)ex , 求出函数的导数,根据函数的单调性证明即可.
,令h(x)=(2﹣x3)ex , 求出函数的导数,根据函数的单调性证明即可.
【考点精析】通过灵活运用利用导数研究函数的单调性和函数的最大(小)值与导数,掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值即可以解答此题.
比较,其中最大的是一个最大值,最小的是最小值即可以解答此题.

 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案【题目】为了调查喜欢旅游是否与性别有关,调查人员就“是否喜欢旅游”这个问题,在火车站分别随机调研了 ![]() 名女性或
名女性或 ![]() 名男性,根据调研结果得到如图所示的等高条形图.
名男性,根据调研结果得到如图所示的等高条形图.
(1)完成下列 ![]() 列联表:
列联表:
喜欢旅游 | 不喜欢旅游 | 估计 | |
女性 | |||
男性 | |||
合计 |
(2)能否在犯错误概率不超过 ![]() 的前提下认为“喜欢旅游与性别有关”.
的前提下认为“喜欢旅游与性别有关”.
附:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
参考公式:![]() ,其中
,其中 ![]()
【题目】电视连续剧《人民的名义》自2017年3月28日在湖南卫视开播以来,引发各方关注,收视率、点击率均占据各大排行榜首位.我们用简单随机抽样的方法对这部电视剧的观看情况进行抽样调查,共调查了600人,得到结果如下:其中图1是非常喜欢《人民的名义》这部电视剧的观众年龄的频率分布直方图;表1是不同年龄段的观众选择不同观看方式的人数.
表1
观看方式 | 电视 | 网络 |
| 150 | 250 |
| 120 | 80 |
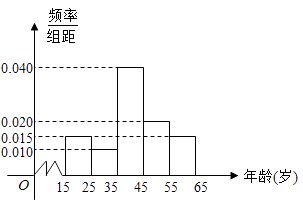
求:(I)假设同一组中的每个数据用该组区间的中点值代替,求非常喜欢《人民的名义》这部电视剧的观众的平均年龄;
(II)根据表1,通过计算说明我们是否有99%的把握认为观看该剧的方式与年龄有关?
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
附: ![]()