[题目]已知椭圆的半焦距为 .原点到经过两点的直线的距离为 . (Ⅰ)求椭圆的离心率,(Ⅱ)如图. 是圆的一条直径.若椭圆经过两点.求椭圆的方程. 题目和参考答案——青夏教育精英家教网—

题目内容

【题目】已知椭圆的半焦距为，原点到经过两点的直线的距离为 .

（Ⅰ）求椭圆的离心率；
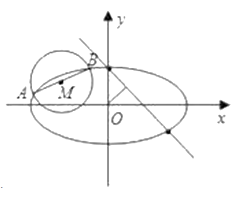
（Ⅱ）如图，是圆的一条直径，若椭圆经过两点，求椭圆的方程.

【答案】解：（Ⅰ）过点的直线方程为，

则原点到直线的距离，

由，得，解得离心率 .

（Ⅱ）由（1）知，椭圆的方程为 .

依题意，圆心是线段的中点，且 .

易知，不与轴垂直.

设其直线方程为，代入（1）得

设，则， .

由，得，解得 .

从而 .

于是 .

由，得，解得 .

故椭圆的方程为 .

【解析】(1)根据题意由点到直线的距离公式可得出代入，联立可求出离心率即可。(2)由(1)设出椭圆的方程再设出直线AB的方程联立，借助韦达定理求出x1 + x2、x1x2关于k的代数式代入到弦长公式中即可求出b2的值，进而得到椭圆的方程。
【考点精析】通过灵活运用点到直线的距离公式和椭圆的标准方程，掌握点到直线的距离为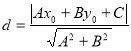：；椭圆标准方程焦点在x轴：，焦点在y轴：即可以解答此题．

练习册系列答案

相关题目

【题目】如图，在四棱锥P﹣ABCD中，底面ABCD为梯形，CD∥AB，AB=2CD，AC交BD于O，锐角△PAD所在平面⊥底面ABCD，PA⊥BD，点Q在侧棱PC上，且PQ=2QC．

（1）求证：PA∥平面QBD；
（2）求证BD⊥AD．

【题目】已知函数的一系列对应值如下表：

（1）根据表格提供的数据求出函数的一个解析式；

（2）根据（1）的结果，若函数的周期为，当时，方程恰有两个不同的解，求实数的取值范围。

【题目】从2017年1月18日开始，支付宝用户可以通过“扫‘福’字”和“参与蚂蚁森林”两种方式获得福卡(爱国福、富强福、和谐福、友善福，敬业福），除夕夜，每一位提前集齐五福的用户都将获得一份现金红包.某髙校一个社团在年后开学后随机调査了80位该校在读大学生，就除夕夜之前是否集齐五福进行了一次调查(若未参与集五福的活动，则也等同于未集齐五福），得到具体数据如下表:

（1）计算这80位大学生集齐五福的频率，并据此估算该校10000名在读大学生中集齐五福的人数；

（2）为了解集齐五福的大学生明年是否愿意继续参加集五福活动，该大学的学生会从集齐五福的学生中，选取2位男生和3位女生逐个进行采访，最后再随机选取3次采访记录放到该大学的官方网站上，求最后被选取的3次采访对象中至少有一位男生的概率.

【题目】已知函数f（x）=x2eax ．
（Ⅰ）当a＜0时，讨论函数f（x）的单调性；
（Ⅱ）在（1）条件下，求函数f（x）在区间[0，1]上的最大值；
（Ⅲ）设函数g（x）=2ex﹣ ，求证：当a=1，对x∈（0，1），g（x）﹣xf（x）＞2恒成立．

【题目】命题p：x∈（﹣∞，0），2x＞3x；命题q：x∈（0，+∞），＞x3；则下列命题中真命题是（）
A.p∧q
B.（￢p）∧q
C.（￢p）∨（￢q）
D.p∧（￢q）

【题目】已知函数， .

（1）求函数的定义域；

（2）判断函数的奇偶性，并说明理由；

（3）判断函数在区间上的单调性，并加以证明.

【题目】函数f（x）=Asin（x+φ）（A＞0，0＜＜4，|φ|＜）过点（0，），且当x= 时，函数f（x）取得最大值1．
（1）将函数f（x）的图象向右平移个单位得到函数g（x），求函数g（x）的表达式；
（2）在（1）的条件下，函数h（x）=f（x）+g（x）+2cos2x﹣1，如果对于x1 ， x2∈R，都有h（x1）≤h（x）≤h（x2），求|x1﹣x2|的最小值．

【题目】若分别为P（1，0）、Q（2，0），R（4，0）、S（8，0）四个点各作一条直线，所得四条直线恰围成正方形，则该正方形的面积不可能为（）
A.
B.
C.
D.

试题分类