题目内容
【题目】某宾馆在装修时,为了美观,欲将客房的窗户设计成半径为1m的圆形,并用四根木条将圆分成如图所示的9个区域,其中四边形ABCD为中心在圆心的矩形,现计划将矩形ABCD区域设计为可推拉的窗口. 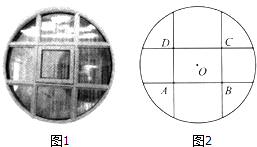
(1)若窗口ABCD为正方形,且面积大于 ![]() m2(木条宽度忽略不计),求四根木条总长的取值范围;
m2(木条宽度忽略不计),求四根木条总长的取值范围;
(2)若四根木条总长为6m,求窗口ABCD面积的最大值.
【答案】
(1)解:设一根木条长为xcm,则正方形的边长为2 ![]() =
= ![]() ,
,
∵SABCD> ![]() ,
,
∴4﹣x2> ![]() ,
,
∴x< ![]() ,
,
∵四根木条将圆分成9个区域,
∴x> ![]() ,
,
∴4 ![]() <x<2
<x<2 ![]() ;
;
(2)解:设AB所在木条长为am,CD所在木条长为bm,
由条件,2a+2b=6,则a+b=3,
∵a,b∈(0,2),
∴b=3﹣a∈(0,2),∴a,b∈(1,2).
∵AB=2 ![]() ,BD=2
,BD=2 ![]() ,
,
∴SABCD=4 ![]()
![]() =
= ![]()
![]() ≤
≤ ![]() ≤
≤ ![]() =
= ![]() ,
,
当且仅当a=b= ![]() ∈(1,2)时,SABCD=
∈(1,2)时,SABCD= ![]() ,
,
答:窗口ABCD面积的最大值为 ![]()
【解析】(1)求出正方形的边长,可得正方形的面积,利用面积大于 ![]() m2 , 即可求四根木条总长的取值范围;(2)设AB所在木条长为am,CD所在木条长为bm,求出AB,BD,可得窗口ABCD面积,利用基本不等式求窗口ABCD面积的最大值.
m2 , 即可求四根木条总长的取值范围;(2)设AB所在木条长为am,CD所在木条长为bm,求出AB,BD,可得窗口ABCD面积,利用基本不等式求窗口ABCD面积的最大值.
【考点精析】利用基本不等式在最值问题中的应用对题目进行判断即可得到答案,需要熟知用基本不等式求最值时(积定和最小,和定积最大),要注意满足三个条件“一正、二定、三相等”.

【题目】为调查某地区老人是否需要志愿者提供帮助,用简单随机抽样方法从该地区调查了500位老年人,结果如下:
是否需要志愿 性别 | 男 | 女 |
需要 | 40 | 30 |
不需要 | 160 | 270 |
- 估计该地区老年人中,需要志愿者提供帮助的老年人的比例;
- 能否有99%的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关?
- 根据(2)的结论,能否提供更好的调查方法来估计该地区老年人,需要志愿帮助的老年人的比例?说明理由
 附:
附:
【题目】某高校共有学生15 000人,其中男生10 500人,女生4500人.为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集300位学生每周平均体育运动时间(单位:h)的样本数据.

(1)应收集多少位女生的样本数据?
(2)根据这300个样本数据,得到学生每周平均体育运动时间的频率分布直方图(如图所示),其中样本数据的分组区间为[0,2],(2,4],(4,6],(6,8],(8,10],(10,12].估计该校学生每周平均体育运动时间超过4 h的概率.
(3)在样本数据中,有60位女生的每周平均体育运动时间超过4 h,请完成下面的2×2列联表,并判断是否有95%的把握认为“该校学生的每周平均体育运动时间与性别有关”?
男生 | 女生 | 总计 | |
每周平均体育运动时间不超过4h | |||
每周平均体育运动时间超过4h | |||
总计 |
附:
P(K2≥k0) | 0.100 | 0.050 | 0.010 | 0.005 |
k0 | 2.706 | 3.841 | 6.635 | 7.879 |
![]()
