题目内容
【题目】在平面直角坐标系xOy中,圆C1:(x﹣1)2+y2=2,圆C2:(x﹣m)2+(y+m)2=m2 . 圆C2上存在点P满足:过点P向圆C1作两条切线PA,PB,切点为A,B,△ABP的面积为1,则正数m的取值范围是 .
【答案】[1, ![]() ]
]
【解析】解:如图,由圆C1:(x﹣1)2+y2=2,圆C2:(x﹣m)2+(y+m)2=m2 ,
得C1(1,0),C2(m,﹣m),
设圆C2上点P,则PA2=PGPC1 ,
而 ![]() ,
,
∴ ![]() ,则
,则 ![]() ,
,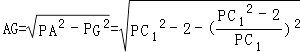 =
= 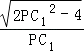 ,
,
∴ 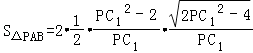 =
= 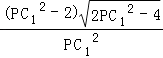 =1.
=1.
令 ![]() ,
,
得t3﹣t2﹣4=0,解得:t=2.
即 ![]() ,∴PC1=2.
,∴PC1=2.
圆C2:(x﹣m)2+(y+m)2=m2上点P到C1距离的最小值为|C1C2|﹣m= ![]() ﹣m,
﹣m,
最大值为|C1C2|+m= ![]() +m,
+m,
由 ![]() ﹣m≤2≤
﹣m≤2≤ ![]() +m,
+m,
得 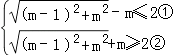 ,
,
解①得: ![]() ,
,
解②得:m≤﹣3或m≥1.
取交集得:1 ![]() .
.
∴正数m得取值范围是[1, ![]() ].
].
所以答案是:[1, ![]() ].
].

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目