题目内容
20.从极点O作一直线与直线l:ρcosθ=4交于点M,在OM上取一点P,使PO•OM=8.(1)以O为坐标原点,极轴为x轴的正半轴,求P点轨迹的直角坐标方程;
(2)设N为l上的任意一点,试求PN的最小值.
分析 (1)设动点P的坐标为(ρ,θ),M的坐标为(ρ0,θ),则ρρ0=12,由ρ0cosθ=4,得到ρ=3cosθ再化为直角坐标方程;
(2)先求出点轨迹的圆心坐标和半径,直线l的直角坐标方程,由点到直线的距离公式求出圆心到直线l的距离,判断出直线与圆的位置关系,即可求出PN的最小值.
解答 解:(1)设动点P的坐标为(ρ,θ),M的坐标为(ρ0,θ),
∵PO•OM=8,∴ρρ0=8,
∵ρ0cosθ=4,∴ρ=2cosθ即为所求的轨迹方程,
∴P点轨迹的直角坐标方程是x2+y2-2x=0;
(2)由(1)知,P点轨迹是以(1,0)为圆心,以1为半径的圆,
∵直线ρcosθ=4在平面直角坐标系中对应的方程为x=4,
∴圆心(1,0)到直线x=4的距离d=4-1=3>1,
∴直线l与圆相离,则PN的最小值是3-1=2.
点评 本题考查动点的轨迹方程的求法,极坐标与直角坐标方程的转化,点到直线的距离公式,考查转化思想的应用,是中档题.

练习册系列答案
相关题目
14.若质点M按规律s(t)=t2运动,则t=2时的瞬时速度为( )
| A. | 1 | B. | 2 | C. | 4 | D. | 6 |
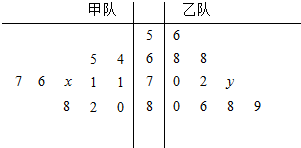 如图的茎叶图记录了甲、乙两代表队各10名同学在一次英语听力比赛中的成绩(单位:分),已知甲代表队数据的中位数为76,乙代表队数据的平均数是75.
如图的茎叶图记录了甲、乙两代表队各10名同学在一次英语听力比赛中的成绩(单位:分),已知甲代表队数据的中位数为76,乙代表队数据的平均数是75.