题目内容
【题目】已知函数![]() .
.
(1)若![]() 在
在![]() 上是减函数,求实数
上是减函数,求实数![]() 的最大值;
的最大值;
(2)若![]() ,求证:
,求证:![]() .
.
【答案】(1)![]() (2)证明见解析
(2)证明见解析
【解析】
(1)根据函数单调性可将问题转化为![]() 在
在![]() 上恒成立问题,通过分离变量的方式将问题转化为
上恒成立问题,通过分离变量的方式将问题转化为![]() ,利用导数求得
,利用导数求得![]() 的最大值,进而得到结果;
的最大值,进而得到结果;
(2)将问题转化为![]() 的证明;利用
的证明;利用![]() 单调递增和零点存在定理可确定存在
单调递增和零点存在定理可确定存在![]() ,使得
,使得![]() ,从而得到
,从而得到![]() ;根据导函数正负可确定
;根据导函数正负可确定![]() 单调性,进而得到
单调性,进而得到![]() ,化简后,结合基本不等式可证得结论.
,化简后,结合基本不等式可证得结论.
由函数解析式可知,![]() 定义域为
定义域为![]() .
.
(1)![]() ,
,
![]() 在
在![]() 上是减函数,
上是减函数,![]() 在
在![]() 上恒成立,即
上恒成立,即![]() 恒成立
恒成立
令![]() ,则
,则![]() ,
,![]() 在
在![]() 上单调递增,
上单调递增,
![]() ,
,![]() ,解得:
,解得:![]() ,
,
![]() 的最大值为
的最大值为![]() .
.
(2)由(1)知:![]() ,则
,则![]() ,
,
![]() 在
在![]() 上单调递增.
上单调递增.
![]() ,当
,当![]() 时,
时,![]() ,
,![]() ,此时
,此时![]() ,
,
![]() 由零点存在定理可知,存在
由零点存在定理可知,存在![]() ,使得
,使得![]() ,即
,即![]() ,
,
![]() .
.
![]() 当
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
![]() 当
当![]() 时,
时,![]() 单调递减;当
单调递减;当![]() 时,
时,![]() 单调递增,
单调递增,

![]() (当且仅当
(当且仅当![]() ,即
,即![]() 时取等号).
时取等号).
![]() 当
当![]() 时,
时,![]() .
.

 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案【题目】广东省的生产总值已经连续30年位居全国第一位,如表是广东省从2012年至2018年7年的生产总值以人民币(单位:万亿元)计算的数据:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
年份代号x | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
广东省生产总值y(单位:万亿元) | 5.71 | 6.25 | 6.78 | 7.28 | 8.09 | 8.97 | 9.73 |
(1)从表中数据可认为x和y的线性相关性较强,求出以x为解释变量、y为预报变量的线性回归方程(系数精确到0.01);
(2)广东省2018年人口约为1.13亿,德国2018年人口约为0.83亿.从人口数量比较看,广东省比德国人口多,但德国2018年的生产总值为4.00万亿美元,以(1)的结论为依据,预测广东省在哪年的生产总值能超过德国在2018年的生产总值?
参考数据:![]() yi=52.81,
yi=52.81,![]() xiyi=230.05,
xiyi=230.05,![]() yi2=411.2153,
yi2=411.2153,![]() xi2=140.
xi2=140.
货币兑换:1美元≈7.03元人民币
参考公式:回归方程![]() x
x![]() 中斜率
中斜率![]() 和截距
和截距![]() 的最小二乘估计公式分别为:
的最小二乘估计公式分别为: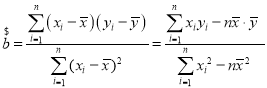 ,
,![]() .
.
【题目】某校为了解高三年级不同性别的学生对体育课改上自习课的态度(肯定还是否定),进行了如下的调查研究.全年级共有![]() 名学生,男女生人数之比为
名学生,男女生人数之比为![]() ,现按分层抽样方法抽取若干名学生,每人被抽到的概率均为
,现按分层抽样方法抽取若干名学生,每人被抽到的概率均为![]() .
.
(1)求抽取的男学生人数和女学生人数;
(2)通过对被抽取的学生的问卷调查,得到如下![]() 列联表:
列联表:
否定 | 肯定 | 总计 | |
男生 | 10 | ||
女生 | 30 | ||
总计 |
①完成列联表;
②能否有![]() 的把握认为态度与性别有关?
的把握认为态度与性别有关?
(3)若一班有![]() 名男生被抽到,其中
名男生被抽到,其中![]() 人持否定态度,
人持否定态度,![]() 人持肯定态度;二班有
人持肯定态度;二班有![]() 名女生被抽到,其中
名女生被抽到,其中![]() 人持否定态度,
人持否定态度,![]() 人持肯定态度.
人持肯定态度.
现从这![]() 人中随机抽取一男一女进一步询问所持态度的原因,求其中恰有一人持肯定态度一人持否定态度的概率.
人中随机抽取一男一女进一步询问所持态度的原因,求其中恰有一人持肯定态度一人持否定态度的概率.
解答时可参考下面临界值表:
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |