题目内容
17.在△ABC中,$\frac{{a}^{3}{+b}^{3}{-c}^{3}}{a+b-c}$=c2,sinA•sinB=$\frac{3}{4}$,则△ABC一定是( )| A. | 等边三角形 | B. | 等腰三角形 | ||
| C. | 直角三角形 | D. | 等腰三角形或直角三角形 |
分析 先把已知等式整理可求得a,b和c的关系,利用余弦定理求得C,通过两角和公式求得cosAcosB的值,最后利用两角和与差的余弦函数求得cos(A-B)=1,判断出A=B,最终判断出三角形的形状.
解答 解:∵$\frac{{a}^{3}{+b}^{3}{-c}^{3}}{a+b-c}$=c2,
∴a3+b3-c3=ac2+bc2-c3,
(a+b)(a2+b2-ab)=(a+b)c2,
∴a2+b2-ab=c2,
∴cosC=$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$=$\frac{1}{2}$,
∴C=$\frac{π}{3}$,
∵sinAsinB=$\frac{3}{4}$,cos(A+B)=cos(180°-C)=cos120°=-$\frac{1}{2}$,
∴cos(A+B)=cosAcosB-sinAsinB,
∴cosAcosB=$\frac{1}{4}$
∴cos(A-B)=cosAcosB+sinAsinB=1.
∵-π<A-B<π,
∴A-B=0.
∴A=B=60°
∴△ABC是等边三角形.
故选:A.
点评 本题主要考查了余弦定理的应用,三角函数恒等变换的应用.解题的关键是找到角与角之间的关系,属于中档题.

练习册系列答案
相关题目
7.(1+i)20-(1-i)20的值为( )
| A. | 0 | B. | 1024 | C. | -1024 | D. | -10241 |
5.角θ的终边过点P(-1,2),则sinθ=( )
| A. | $\frac{\sqrt{5}}{5}$ | B. | $\frac{2\sqrt{5}}{5}$ | C. | -$\frac{\sqrt{5}}{5}$ | D. | -$\frac{2\sqrt{5}}{5}$ |
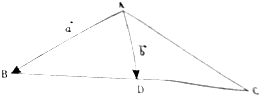 如图,在△ABC中,D为BC中点,记$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,已知|$\overrightarrow{a}$|=2,|$\overrightarrow{b}$|=1,<$\overrightarrow{a}$,$\overrightarrow{b}$>=$\frac{π}{3}$.
如图,在△ABC中,D为BC中点,记$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,已知|$\overrightarrow{a}$|=2,|$\overrightarrow{b}$|=1,<$\overrightarrow{a}$,$\overrightarrow{b}$>=$\frac{π}{3}$.