题目内容
【题目】(已知数列{![]() }满足:
}满足:![]() ,
,![]() 为数列
为数列![]() 的前
的前![]() 项和.
项和.
(1) 若{![]() }是递增数列,且
}是递增数列,且![]() 成等差数列,求
成等差数列,求![]() 的值;
的值;
(2) 若![]() ,且{
,且{![]() }是递增数列,{
}是递增数列,{![]() }是递减数列,求数列{
}是递减数列,求数列{![]() }的通项公式;
}的通项公式;
(3) 若![]() ,对于给定的正整数
,对于给定的正整数![]() ,是否存在一个满足条件的数列
,是否存在一个满足条件的数列![]() ,使得
,使得![]() ,如果存在,给出一个满足条件的数列,如果不存在,请说明理由.
,如果存在,给出一个满足条件的数列,如果不存在,请说明理由.
【答案】(1)![]() (2)
(2)![]() (3)详见解析
(3)详见解析
【解析】
(1)因为![]() 是递增数列,所以
是递增数列,所以![]() .而
.而![]() ,因此又
,因此又![]() 成等差数列,所以
成等差数列,所以![]() ,因而
,因而![]() ,解得
,解得![]()
当![]() 时,
时,![]() ,这与
,这与![]() 是递增数列矛盾,故
是递增数列矛盾,故![]() .
.
(2)由于![]() 是递增数列,因而
是递增数列,因而![]() ,于是
,于是
但![]() ,所以
,所以![]() ①
①
![]() . ②
. ②
由①,②知,![]() ,
,
因此![]() ③
③
因为![]() 是递减数列,同理可得,
是递减数列,同理可得,![]() ,
,
故![]() ④
④
由③,④即知,![]() .
.
于是![]()
![]()
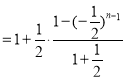
![]() .
.
故数列![]() 的通项公式为
的通项公式为![]()
(3)令![]()
因为![]() ,……,
,……,![]()
所以![]()
![]()
因为![]()
所以![]() 为偶数,
为偶数,
所以要使![]() 为偶数,
为偶数,
即4整除![]() .
.
当![]() :
:
![]()
![]() 时,有
时,有![]()
当![]() 不能被4整除,
不能被4整除,
此时不存在数列![]() ,使得
,使得![]() .
.

【题目】至2018年底,我国发明专利申请量已经连续8年位居世界首位,下表是我国2012年至2018年发明专利申请量以及相关数据.
总计 | ||||||||
年代代码 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 28 |
申请量 | 65 | 82 | 92 | 110 | 133 | 138 | 154 | 774 |
| 65 | 164 | 276 | 440 | 665 | 828 | 1078 | 3516 |
注:年代代码1~7分别表示2012~2018.
(1)可以看出申请量每年都在增加,请问这几年中那一年的增长率达到最高,最高是多少?
(2)建立![]() 关于
关于![]() 的回归直线方程(精确到0.01),并预测我国发明专利申请量突破200万件的年份.
的回归直线方程(精确到0.01),并预测我国发明专利申请量突破200万件的年份.
参考公式: .
.
【题目】某茶楼有四类茶饮,假设为顾客准备泡茶工具所需的时间互相独立,且都是整数分钟,经统计以往为100位顾客准备泡茶工具所需的时间![]() ,结果如下:
,结果如下:
类别 | 铁观音 | 龙井 | 金骏眉 | 大红袍 |
顾客数(人) | 20 | 30 | 40 | 10 |
时间 | 2 | 3 | 4 | 6 |
注:服务员在准备泡茶工具时的间隔时间忽略不计,并将频率视为概率.
(1)求服务员恰好在第6分种开始准备第三位顾客的泡茶工具的概率;
(2)用![]() 表示至第4分钟末已准备好了工具的顾客人数,求
表示至第4分钟末已准备好了工具的顾客人数,求![]() 的分布列及数学期望.
的分布列及数学期望.