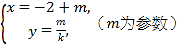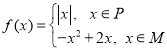题目内容
【题目】己知函数![]() .
.
(1)当![]() 时,求曲线
时,求曲线![]() 在
在![]() 处的切线方程:
处的切线方程:
(2)当![]() >0时,求函数
>0时,求函数![]() 的单调区间和极值;
的单调区间和极值;
(3)当![]() 时,不等式
时,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1) ![]() ;(2)
;(2) ![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() 和
和![]() .极小值为
.极小值为![]() ,极大值为
,极大值为![]() ;(3)
;(3) ![]()
【解析】
(1)求出切点坐标,切线斜率,可得曲线![]() 在
在![]() 处的切线方程;
处的切线方程;
(2)求导函数,利用导数的正负,可得函数的单调区间,从而可得函数的极值;
(3)求出![]() 在区间
在区间![]() 上的最大值与最小值,利用当
上的最大值与最小值,利用当![]() 时,不等式
时,不等式
![]() 恒成立,再列出不等式求解即可.
恒成立,再列出不等式求解即可.
(1) 当![]() 时,
时,![]() ,
, ![]() ,
,
故![]() .又
.又![]() ,
,
故曲线![]() 在
在![]() 处的切线方程为
处的切线方程为![]() ,化简得
,化简得![]() .
.
(2)![]() .
.
令![]() 有
有![]() ,
,![]() .当
.当![]() 时有
时有![]() ,
,
故![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() 和
和![]() .
.
当![]() 时取得极小值
时取得极小值![]() ,
,
当![]() 时取得极大值
时取得极大值![]() .
.
(3)由(2),![]() ,
,
故![]() 在
在![]() 上单调递减.
上单调递减.
当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() .故
.故![]()
又因为当![]() 时,不等式
时,不等式![]() 恒成立.故
恒成立.故![]() 恒成立.
恒成立.
所以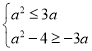 解得
解得![]() .
.
故![]() 的范围为
的范围为![]() .
.

 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案【题目】某保险公司利用简单随机抽样方法,对投保车辆进行抽样,样本车辆中每辆车的赔付结果统计如下:
赔付金额(元) | 0 | 1 000 | 2 000 | 3 000 | 4 000 |
车辆数(辆) | 500 | 130 | 100 | 150 | 120 |
(1)若每辆车的投保金额均为2800元,估计赔付金额大于投保金额的概率.
(2)在样本车辆中,车主是新司机的占10%,在赔付金额为4000元的样本车辆中,车主是新司机的占20%,估计在已投保车辆中,新司机获赔金额为4000元的概率.
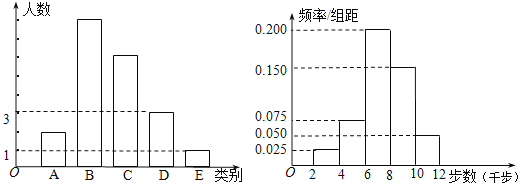
【题目】“微信运动”是手机![]() 推出的多款健康运动软件中的一款,大学生
推出的多款健康运动软件中的一款,大学生![]() 的微信好友中有400位好友参与了“微信运动”.他随机抽取了40位参与“微信运动”的微信好友(女20人,男20人)在某天的走路步数,经统计,其中女性好友走路的步数情况可分为五个类别:
的微信好友中有400位好友参与了“微信运动”.他随机抽取了40位参与“微信运动”的微信好友(女20人,男20人)在某天的走路步数,经统计,其中女性好友走路的步数情况可分为五个类别:![]() 、0~2000步,(说明:“0~2000”表示“大于或等于0,小于2000”,以下同理),
、0~2000步,(说明:“0~2000”表示“大于或等于0,小于2000”,以下同理),![]() 、2000~5000步,
、2000~5000步,![]() 、5000~8000步,
、5000~8000步,![]() 、8000~10000步,
、8000~10000步,![]() 、10000~12000步,且
、10000~12000步,且![]() 三种类别的人数比例为
三种类别的人数比例为![]() ,将统计结果绘制如图所示的柱形图;男性好友走路的步数数据绘制如图所示的频率分布直方图.
,将统计结果绘制如图所示的柱形图;男性好友走路的步数数据绘制如图所示的频率分布直方图.
参与者 | 超越者 | 合计 | |
男 | 20 | ||
女 | 20 | ||
合计 | 40 |
若某人一天的走路步数大于或等于8000,则被系统认定为“超越者”,否则被系统认定为“参与者”.
(Ⅰ)若以大学生![]() 抽取的微信好友在该天行走步数的频率分布,作为参与“微信运动”的所有微信好友每天走路步数的概率分布,试估计大学生
抽取的微信好友在该天行走步数的频率分布,作为参与“微信运动”的所有微信好友每天走路步数的概率分布,试估计大学生![]() 的参与“微信运动”的400位微信好友中,每天走路步数在
的参与“微信运动”的400位微信好友中,每天走路步数在
(Ⅱ)若在大学生![]() 该天抽取的步数在8000~12000的微信好友中,按男女比例分层抽取9人进行身体状况调查,然后再从这9位微信好友中随机抽取4人进行采访,求其中至少有一位女性微信好友被采访的概率;
该天抽取的步数在8000~12000的微信好友中,按男女比例分层抽取9人进行身体状况调查,然后再从这9位微信好友中随机抽取4人进行采访,求其中至少有一位女性微信好友被采访的概率;
(Ⅲ)请根据抽取的样本数据完成下面的![]() 列联表,并据此判断能否有
列联表,并据此判断能否有![]() 的把握认为“认定类别”与“性别”有关?
的把握认为“认定类别”与“性别”有关?