题目内容
过椭圆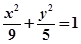 的左焦点F的直线
的左焦点F的直线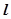 交椭圆于点A、B,交其左准线于点C,
交椭圆于点A、B,交其左准线于点C,
若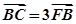 ,则此直线的斜率为
,则此直线的斜率为
A、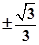 B、
B、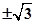 C、
C、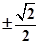 D、
D、
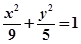 的左焦点F的直线
的左焦点F的直线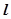 交椭圆于点A、B,交其左准线于点C,
交椭圆于点A、B,交其左准线于点C,若
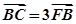 ,则此直线的斜率为
,则此直线的斜率为 A、
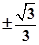 B、
B、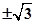 C、
C、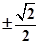 D、
D、
B
先求出焦点坐标和准线方程,利用直角三角形相似求出点B到左准线的距离为h,求出点B的横坐标,再把点B的横坐标代入椭圆的方程求得B的纵坐标,得到点B的坐标,由斜率公式求出直线I的斜率.
解答:解:椭圆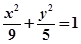 的左焦点F(-2,0),左准线方程为 x=-
的左焦点F(-2,0),左准线方程为 x=- ,
,
 =3
=3 ,且
,且 与
与 同向,
同向,
故 =3,设|FB|=k,则|BC|=3k,设点B到左准线的距离为h,由三角形全等得
=3,设|FB|=k,则|BC|=3k,设点B到左准线的距离为h,由三角形全等得 =
= ,
,
即 ,h=
,h= ,∴xB=-
,∴xB=- ,∴B(-
,∴B(-
由点B、点F的坐标,用两点表示的斜率公式求出直线I的斜率为± ,
,
故选B.
解答:解:椭圆
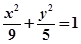 的左焦点F(-2,0),左准线方程为 x=-
的左焦点F(-2,0),左准线方程为 x=- ,
, =3
=3 ,且
,且 与
与 同向,
同向,故
 =3,设|FB|=k,则|BC|=3k,设点B到左准线的距离为h,由三角形全等得
=3,设|FB|=k,则|BC|=3k,设点B到左准线的距离为h,由三角形全等得 =
= ,
,即
 ,h=
,h= ,∴xB=-
,∴xB=- ,∴B(-
,∴B(-
由点B、点F的坐标,用两点表示的斜率公式求出直线I的斜率为±
 ,
,故选B.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
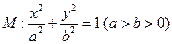 的左右焦点分别
的左右焦点分别 为
为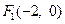 ,
,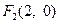 .在椭圆
.在椭圆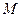 中有一内接三角形
中有一内接三角形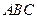 ,其顶点
,其顶点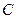 的坐
的坐 标
标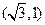 ,
,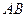 所在直线的斜率为
所在直线的斜率为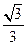 .
.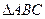 的面积最大时,求直线
的面积最大时,求直线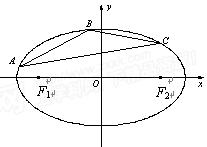
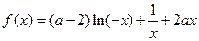 (
(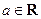 ).
).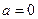 时,求
时,求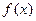 的极值;
的极值;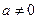 时,求
时,求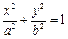
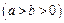 上任意两点
上任意两点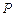 ,
,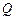 ,若
,若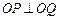 ,则乘积
,则乘积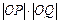 的最小值为 .
的最小值为 .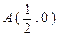 ,点
,点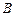 在直线
在直线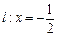 上运动,过点
上运动,过点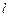 垂直的直线和
垂直的直线和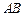 的中垂线相交于点
的中垂线相交于点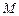 .
.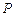 的方程;
的方程;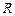 ,
,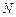 在
在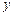 轴上,圆
轴上,圆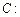
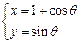 (
(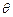 为参数)内切于
为参数)内切于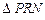 ,求
,求 是双曲线
是双曲线 的左、右焦点,过
的左、右焦点,过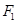 且垂直于
且垂直于 轴的直线与双曲线交于
轴的直线与双曲线交于 两点,若
两点,若 为钝角三角形,则该双曲线的离心率
为钝角三角形,则该双曲线的离心率 的取值范围是( )
的取值范围是( )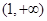



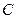 过点
过点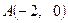 ,且与
,且与 圆
圆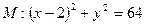 相内切.
相内切.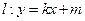 (其中
(其中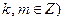 与(1)中所求轨迹交于不同两点
与(1)中所求轨迹交于不同两点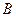 ,D
,D ,与双曲线
,与双曲线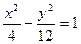 交于不同两点
交于不同两点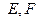 ,问是否存在直线
,问是否存在直线 ,使得向量
,使得向量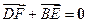 ,若存在,指出这样的直线有多少条?若不存在,请说明理由.
,若存在,指出这样的直线有多少条?若不存在,请说明理由.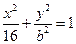
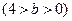 .P为椭圆上的动点,
.P为椭圆上的动点,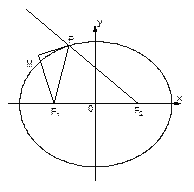
 、
、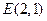 ,
,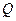 :
: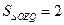 ?
? ,则双曲线的离心率为( )
,则双曲线的离心率为( )

