题目内容
(本题满分13分)
已知椭圆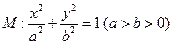 的左右焦点分别
的左右焦点分别 为
为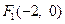 ,
,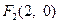 .在椭圆
.在椭圆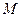 中有一内接三角形
中有一内接三角形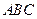 ,其顶点
,其顶点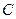 的坐
的坐 标
标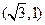 ,
,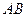 所在直线的斜率为
所在直线的斜率为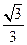 .
.
(Ⅰ)求椭圆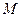 的方程;
的方程;
(Ⅱ)当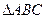 的面积最大时,求直线
的面积最大时,求直线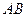 的方程.
的方程.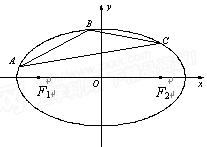
已知椭圆
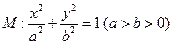 的左右焦点分别
的左右焦点分别 为
为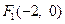 ,
,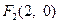 .在椭圆
.在椭圆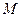 中有一内接三角形
中有一内接三角形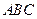 ,其顶点
,其顶点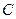 的坐
的坐 标
标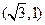 ,
,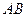 所在直线的斜率为
所在直线的斜率为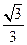 .
.(Ⅰ)求椭圆
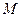 的方程;
的方程;(Ⅱ)当
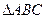 的面积最大时,求直线
的面积最大时,求直线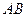 的方程.
的方程.
(1) (2)
(2)
 (2)
(2)
(Ⅰ)由椭圆的定义知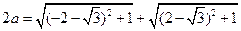 .
.
解得 ,所以
,所以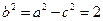 .
.
所以椭圆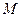 的方程为
的方程为 .………………………………………………4分
.………………………………………………4分
(Ⅱ)由题意设直线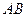 的方程为
的方程为 ,
,
由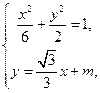 得
得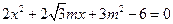 .
.
因为直线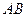 与椭圆
与椭圆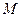 交于不同的两点
交于不同的两点 ,且点
,且点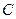 不在直线
不在直线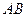 上,
上,
所以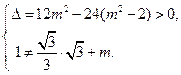 解得
解得 ,且
,且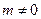 .
.
设 两点的坐标分别为
两点的坐标分别为 ,
, ,
,
则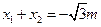 ,
,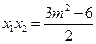 ,
,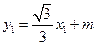 ,
, .
.
所以 .
.
点 到直线
到直线 的距离
的距离 .
.
于是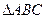 的面积
的面积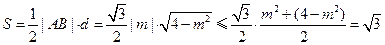 ,
,
当且仅当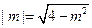 ,即
,即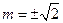 时
时 成立.
成立.
所以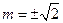 时
时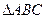 的面积最大,此时直线
的面积最大,此时直线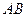 的方程为
的方程为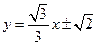 .
.
即为 .……………………………………………………………13分
.……………………………………………………………13分
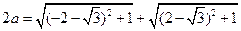 .
.解得
 ,所以
,所以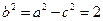 .
.所以椭圆
 的方程为
的方程为 .………………………………………………4分
.………………………………………………4分(Ⅱ)由题意设直线
 的方程为
的方程为 ,
,由
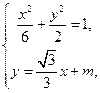 得
得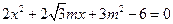 .
.因为直线
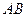 与椭圆
与椭圆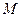 交于不同的两点
交于不同的两点 ,且点
,且点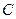 不在直线
不在直线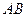 上,
上,所以
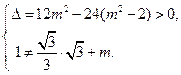 解得
解得 ,且
,且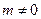 .
.设
 两点的坐标分别为
两点的坐标分别为 ,
, ,
,则
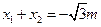 ,
,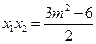 ,
,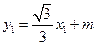 ,
, .
.所以
 .
.点
 到直线
到直线 的距离
的距离 .
.于是
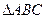 的面积
的面积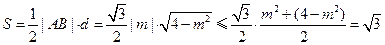 ,
,当且仅当
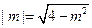 ,即
,即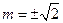 时
时 成立.
成立.所以
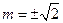 时
时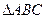 的面积最大,此时直线
的面积最大,此时直线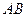 的方程为
的方程为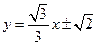 .
.即为
 .……………………………………………………………13分
.……………………………………………………………13分
练习册系列答案
相关题目

 的离心率为
的离心率为 ,以原点为圆心,椭圆的短半轴为半径的圆与直线
,以原点为圆心,椭圆的短半轴为半径的圆与直线 相切.
相切. 的方程;
的方程;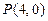 ,
, ,
,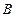 是椭圆
是椭圆 轴对称的任意两个不同的点,连结
轴对称的任意两个不同的点,连结 交椭圆
交椭圆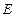 ,证明直线
,证明直线 与
与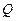 ;
; ,
,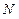 两点,求
两点,求 的取值范围.
的取值范围.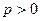 ,动点
,动点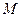 到定点
到定点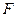
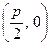 的距离比
的距离比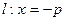 的距离小
的距离小 .
.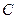 的方程;
的方程;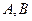 是轨迹
是轨迹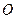 的两个不同点,
的两个不同点,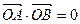 ,求
,求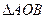 面积的最小值;
面积的最小值;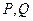 关于直线
关于直线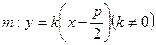 对称?若存在,求出直线
对称?若存在,求出直线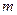 的方程,若不存在,说明理由.
的方程,若不存在,说明理由. 的两个顶点坐标A
的两个顶点坐标A 、B
、B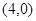 ,
,



 的左焦点F的直线
的左焦点F的直线 交椭圆于点A、B,交其左准线于点C,
交椭圆于点A、B,交其左准线于点C, ,则此直线的斜率为
,则此直线的斜率为  B、
B、 C、
C、 D、
D、
 直线y=x+1与曲线
直线y=x+1与曲线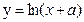 相切,则
相切,则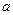 的值为( )
的值为( ) 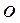 为坐标原点,△
为坐标原点,△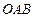 和△
和△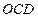 均为正三角形,点
均为正三角形,点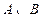 在抛物线
在抛物线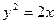 上,点
上,点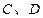 在抛物线
在抛物线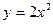 上,则△
上,则△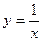 上一点A(1,1),则该曲线
上一点A(1,1),则该曲线