题目内容
(本题满分12分)
已知动圆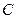 过点
过点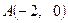 ,且与
,且与 圆
圆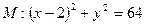 相内切.
相内切.
(1)求动圆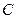 的圆心的轨迹方程;
的圆心的轨迹方程;
(2)设直线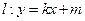 (其中
(其中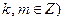 与(1)中所求轨迹交于不同两点
与(1)中所求轨迹交于不同两点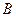 ,D
,D ,与双曲线
,与双曲线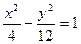 交于不同两点
交于不同两点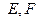 ,问是否存在直线
,问是否存在直线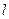 ,使得向量
,使得向量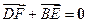 ,若存在,指出这样的直线有多少条?若不存在,请说明理由.
,若存在,指出这样的直线有多少条?若不存在,请说明理由.
已知动圆
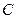 过点
过点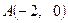 ,且与
,且与 圆
圆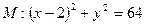 相内切.
相内切.(1)求动圆
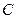 的圆心的轨迹方程;
的圆心的轨迹方程;(2)设直线
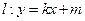 (其中
(其中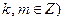 与(1)中所求轨迹交于不同两点
与(1)中所求轨迹交于不同两点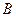 ,D
,D ,与双曲线
,与双曲线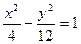 交于不同两点
交于不同两点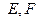 ,问是否存在直线
,问是否存在直线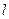 ,使得向量
,使得向量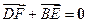 ,若存在,指出这样的直线有多少条?若不存在,请说明理由.
,若存在,指出这样的直线有多少条?若不存在,请说明理由.解:(1)圆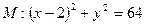 ,圆心
,圆心 的坐标为
的坐标为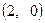 ,半径
,半径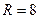 .
.
∵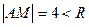 ,∴点
,∴点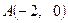 在圆
在圆 内.
内.
设动圆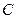 的半径为
的半径为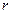 ,圆心为
,圆心为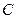 ,依题意得
,依题意得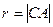 ,且
,且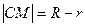 ,
,
即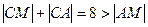 .
.
∴圆心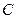 的轨迹是中心在原点,以
的轨迹是中心在原点,以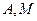 两点为焦点,长轴长为
两点为焦点,长轴长为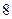 的椭圆,设其方程为
的椭圆,设其方程为
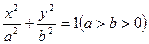 , 则
, 则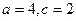 .∴
.∴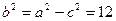 .
.
∴所求动圆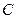 的圆心的轨迹方程为
的圆心的轨迹方程为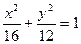 .…………………………………4分
.…………………………………4分
(2)由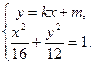 消去
消去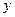 化简整理得:
化简整理得: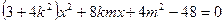
设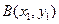 ,
,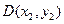 ,则
,则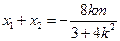 ……………………………………6分
……………………………………6分
△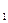
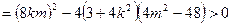 .①
.①
由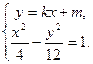 消去
消去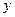 化简整理得:
化简整理得: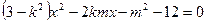 .
.
设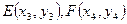 ,则
,则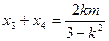 ,
,
△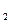
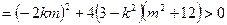 .② ……………………………………8分
.② ……………………………………8分
∵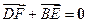 ,∴
,∴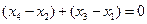 ,即
,即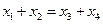 ,
,
∴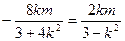 .∴
.∴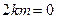 或
或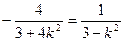 .
.
解得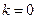 或
或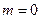 ……… 10分
……… 10分
当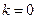 时,由①、②得
时,由①、②得 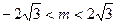 ,
,
∵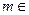 Z,,∴
Z,,∴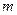 的值为
的值为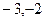
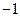 ,
,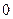 ,
,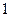
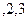 ;
;
当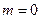 ,由①、②得
,由①、②得 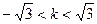 ,
,
∵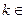 Z,,∴
Z,,∴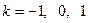 .
.
∴满足条件的直线共有9条.………………………………………………12分
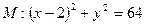 ,圆心
,圆心 的坐标为
的坐标为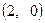 ,半径
,半径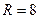 .
.∵
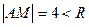 ,∴点
,∴点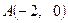 在圆
在圆 内.
内. 设动圆
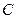 的半径为
的半径为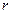 ,圆心为
,圆心为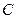 ,依题意得
,依题意得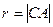 ,且
,且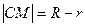 ,
,即
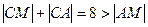 .
. ∴圆心
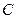 的轨迹是中心在原点,以
的轨迹是中心在原点,以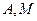 两点为焦点,长轴长为
两点为焦点,长轴长为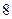 的椭圆,设其方程为
的椭圆,设其方程为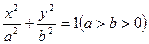 , 则
, 则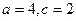 .∴
.∴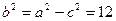 .
.∴所求动圆
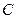 的圆心的轨迹方程为
的圆心的轨迹方程为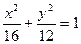 .…………………………………4分
.…………………………………4分(2)由
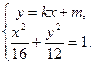 消去
消去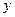 化简整理得:
化简整理得: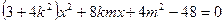
设
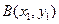 ,
,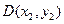 ,则
,则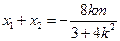 ……………………………………6分
……………………………………6分△
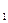
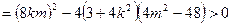 .①
.①由
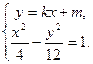 消去
消去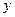 化简整理得:
化简整理得: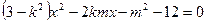 .
.设
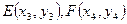 ,则
,则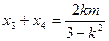 ,
,△
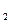
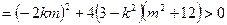 .② ……………………………………8分
.② ……………………………………8分∵
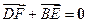 ,∴
,∴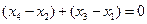 ,即
,即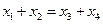 ,
,∴
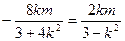 .∴
.∴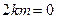 或
或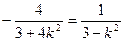 .
.解得
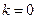 或
或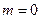 ……… 10分
……… 10分 当
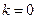 时,由①、②得
时,由①、②得 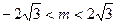 ,
,∵
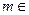 Z,,∴
Z,,∴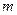 的值为
的值为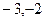
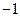 ,
,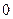 ,
,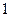
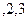 ;
;当
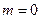 ,由①、②得
,由①、②得 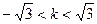 ,
,∵
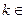 Z,,∴
Z,,∴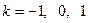 .
.∴满足条件的直线共有9条.………………………………………………12分
略

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

 的离心率为
的离心率为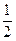 ,以原点为圆心,椭圆的短半轴为半径的圆与直线
,以原点为圆心,椭圆的短半轴为半径的圆与直线 相切.
相切. 的方程;
的方程; ,
, ,
, 是椭圆
是椭圆 轴对称的任意两个不同的点,连结
轴对称的任意两个不同的点,连结 交椭圆
交椭圆 ,证明直线
,证明直线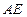 与
与 ;
; ,
, 两点,求
两点,求 的取值范围.
的取值范围.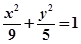 的左焦点F的直线
的左焦点F的直线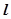 交椭圆于点A、B,交其左准线于点C,
交椭圆于点A、B,交其左准线于点C,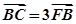 ,则此直线的斜率为
,则此直线的斜率为 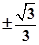 B、
B、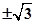 C、
C、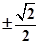 D、
D、
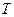 :
: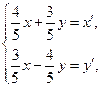 可把平面直角坐标系上的一点
可把平面直角坐标系上的一点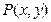 变换到这一平面上的一点
变换到这一平面上的一点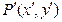 .
.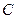 的中心为坐标原点,焦点在
的中心为坐标原点,焦点在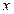 轴上,且焦距为
轴上,且焦距为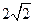 ,长轴顶点和短轴顶点间的距离为2. 求该椭圆
,长轴顶点和短轴顶点间的距离为2. 求该椭圆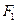 、
、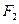 经变换公式
经变换公式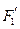 和
和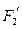 的坐标;
的坐标;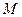 上一点
上一点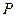 经变换公式
经变换公式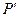 与点
与点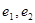 分别为具有公共焦点
分别为具有公共焦点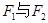 的椭圆和双曲线的离心率,P为两曲线的一个公共点,且满足
的椭圆和双曲线的离心率,P为两曲线的一个公共点,且满足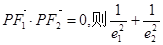 的值为 ( )
的值为 ( )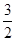
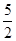
 中,
中, ,且
,且 。现建立以A点为坐标原点,以
。现建立以A点为坐标原点,以 的平分线所在直线为x轴的平面直角坐标系,如图所示。
的平分线所在直线为x轴的平面直角坐标系,如图所示。 的值。
的值。
 与双曲线
与双曲线 的焦点相同,则
的焦点相同,则 .
. 的左、右焦点分别为
的左、右焦点分别为 ,其一条渐近线方程为
,其一条渐近线方程为 ,点
,点 在该双曲线上,则
在该双曲线上,则