题目内容
(本小题共14分)
设函数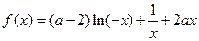 (
(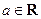 ).
).
(Ⅰ)当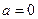 时,求
时,求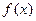 的极值;
的极值;
(Ⅱ)当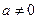 时,求
时,求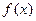 的单调区间.
的单调区间.
设函数
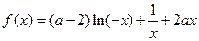 (
(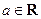 ).
).(Ⅰ)当
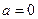 时,求
时,求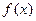 的极值;
的极值;(Ⅱ)当
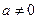 时,求
时,求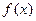 的单调区间.
的单调区间. (Ⅰ)当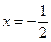 时,
时,  取得极大值为
取得极大值为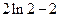 .
.
(Ⅱ)当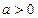 时,
时, 的增区间为
的增区间为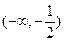 ,减区间为
,减区间为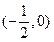 ;
;
当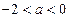 时,
时, 的增区间为
的增区间为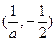 ,减区间为
,减区间为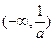 ,
,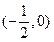 ;
;
当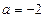 时,
时, 的减区间为
的减区间为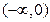 ,无增区间;
,无增区间;
当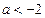 时,
时, 的增区间为
的增区间为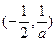 ,减区间为
,减区间为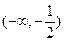 ,
,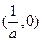 .
.
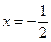 时,
时,  取得极大值为
取得极大值为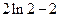 .
.(Ⅱ)当
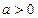 时,
时, 的增区间为
的增区间为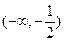 ,减区间为
,减区间为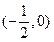 ;
;当
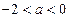 时,
时, 的增区间为
的增区间为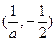 ,减区间为
,减区间为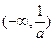 ,
,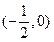 ;
;当
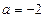 时,
时, 的减区间为
的减区间为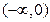 ,无增区间;
,无增区间;当
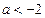 时,
时, 的增区间为
的增区间为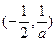 ,减区间为
,减区间为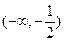 ,
,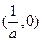 .
.(Ⅰ)依题意,知 的定义域为
的定义域为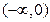 .
.
当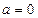 时,
时,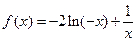 ,
,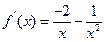
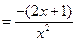 .
.
令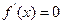 ,解得
,解得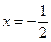 .
.
当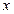 变化时,
变化时,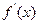 与
与 的变化情况如下表:
的变化情况如下表:
由上表知:当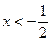 时,
时,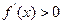 ;当
;当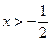 时,
时,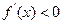 .
.
故当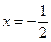 时,
时,  取得极大值为
取得极大值为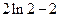 .-------------------5分
.-------------------5分
(Ⅱ)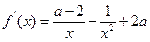
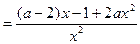
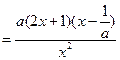
若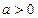 ,令
,令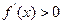 ,解得:
,解得: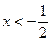 ;令
;令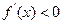 ,解得:
,解得: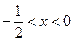 .
.
若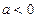 ,①当
,①当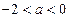 时,
时,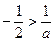
令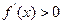 ,解得:
,解得: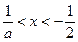 ;
;
令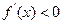 ,解得:
,解得: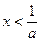 或
或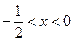 .
.
②当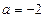 时,
时,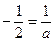 ,
,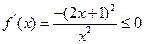
③当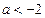 时,
时,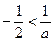
令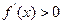 ,解得:
,解得: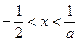 ;
;
令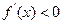 ,解得:
,解得: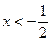 或
或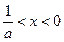 .
.
综上,当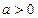 时,
时, 的增区间为
的增区间为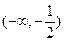 ,减区间为
,减区间为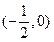 ;
;
当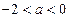 时,
时, 的增区间为
的增区间为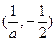 ,减区间为
,减区间为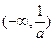 ,
,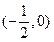 ;
;
当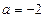 时,
时, 的减区间为
的减区间为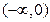 ,无增区间;
,无增区间;
当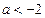 时,
时, 的增区间为
的增区间为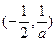 ,减区间为
,减区间为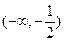 ,
,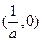 .
.
 的定义域为
的定义域为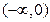 .
.当
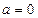 时,
时,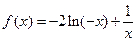 ,
,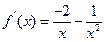
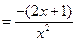 .
.令
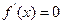 ,解得
,解得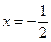 .
.当
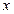 变化时,
变化时,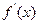 与
与 的变化情况如下表:
的变化情况如下表: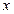 | 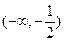 | 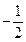 | 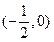 |
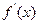 | 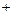 | 0 | 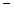 |
 | 单调递增 | 极大值 | 单调递减 |
由上表知:当
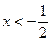 时,
时,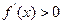 ;当
;当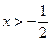 时,
时,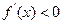 .
.故当
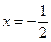 时,
时,  取得极大值为
取得极大值为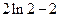 .-------------------5分
.-------------------5分(Ⅱ)
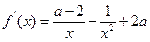
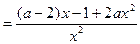
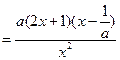
若
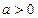 ,令
,令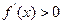 ,解得:
,解得: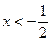 ;令
;令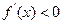 ,解得:
,解得: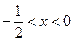 .
.若
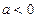 ,①当
,①当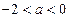 时,
时,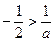
令
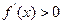 ,解得:
,解得: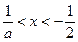 ;
;令
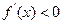 ,解得:
,解得: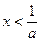 或
或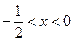 .
.②当
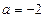 时,
时,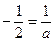 ,
,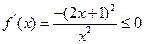
③当
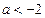 时,
时,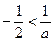
令
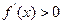 ,解得:
,解得: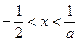 ;
;令
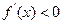 ,解得:
,解得: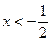 或
或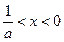 .
.综上,当
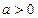 时,
时, 的增区间为
的增区间为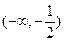 ,减区间为
,减区间为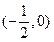 ;
;当
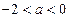 时,
时, 的增区间为
的增区间为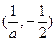 ,减区间为
,减区间为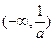 ,
,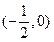 ;
;当
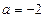 时,
时, 的减区间为
的减区间为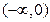 ,无增区间;
,无增区间;当
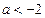 时,
时, 的增区间为
的增区间为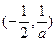 ,减区间为
,减区间为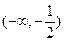 ,
,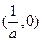 .
.
练习册系列答案
相关题目
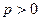 ,动点
,动点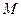 到定点
到定点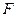
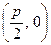 的距离比
的距离比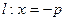 的距离小
的距离小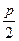 .
.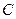 的方程;
的方程;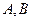 是轨迹
是轨迹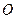 的两个不同点,
的两个不同点,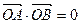 ,求
,求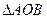 面积的最小值;
面积的最小值;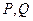 关于直线
关于直线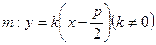 对称?若存在,求出直线
对称?若存在,求出直线 的方程,若不存在,说明理由.
的方程,若不存在,说明理由.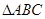 的两个顶点坐标A
的两个顶点坐标A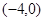 、B
、B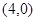 ,
,



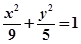 的左焦点F的直线
的左焦点F的直线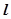 交椭圆于点A、B,交其左准线于点C,
交椭圆于点A、B,交其左准线于点C,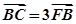 ,则此直线的斜率为
,则此直线的斜率为 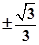 B、
B、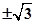 C、
C、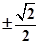 D、
D、
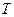 :
: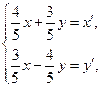 可把平面直角坐标系上的一点
可把平面直角坐标系上的一点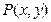 变换到这一平面上的一点
变换到这一平面上的一点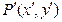 .
.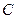 的中心为坐标原点,焦点在
的中心为坐标原点,焦点在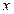 轴上,且焦距为
轴上,且焦距为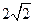 ,长轴顶点和短轴顶点间的距离为2. 求该椭圆
,长轴顶点和短轴顶点间的距离为2. 求该椭圆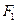 、
、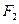 经变换公式
经变换公式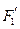 和
和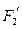 的坐标;
的坐标;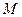 上一点
上一点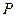 经变换公式
经变换公式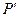 与点
与点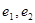 分别为具有公共焦点
分别为具有公共焦点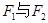 的椭圆和双曲线的离心率,P为两曲线的一个公共点,且满足
的椭圆和双曲线的离心率,P为两曲线的一个公共点,且满足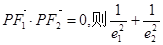 的值为 ( )
的值为 ( )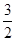
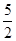
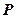 是双曲线
是双曲线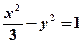 的右支上一动点,F是双曲线的右焦点,已知
的右支上一动点,F是双曲线的右焦点,已知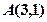 ,则
,则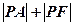 的最小值是 ( )
的最小值是 ( )



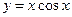 在
在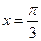 处的切线的斜率是( )
处的切线的斜率是( )


