Question

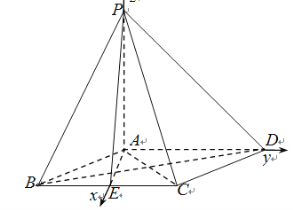
【题目】在四棱锥中，底面是边长为的菱形，，.

（1）证明：平面；

（2）若，求二面角 的余弦值.

Answer 1

【答案】（1）见解析；（2）

【解析】

试题分析：（1）连接，取中点，连接，然后根据等腰三角形的性质得出，，从而推出平面，进而利用线面垂直的性质定理结合判定定理可使问题得证；（2）以为原点，建立空间直角坐标系，然后求得相关点的坐标与向量，由此求得平面与平面的法向量，从而利用空间夹角公式求解.

试题解析：连接AC，则△ABC和△ACD都是正三角形，取BC中点E，连接AE，PE，

因为E为BC的中点，所以在△ABC中，，

因为PB＝PC，所以BC⊥PE，

又因为PE∩AE＝E，所以BC⊥平面PAE，

又PA平面PAE，所以BC⊥PA.

同理CD⊥PA，

又因为BC∩CD＝C，所以PA⊥平面ABCD. …6

（2）如图，以A为原点，建立空间直角坐标系A-xyz，

则B(，－1，0)，D(0，2，0)，P(0，0，2)，＝(0，2，－2)，＝(－，3，0)，

设平面PBD的法向量为m＝(x，y，z)，则即

取平面PBD的法向量m＝(，1，1)， …9分

取平面PAD的法向量n＝(1，0，0)，则cosm，n＝＝，

所以二面角A-PD-B的余弦值是. …12分