题目内容
设函数f（x）满足f（-x）=-f（x）（x∈R），且在（0，+∞）上为增函数，且f（1）=0，则不等式
≤0的解集为______．
| f(x)-f(-x) |
| x |
∵函数f（x）满足f（-x）=-f（x）（x∈R），
∴f（x）-f（-x）=f（x）+f（x）=2f（x），
因此，不等式
≤0等价于
≤0，
化简得
或
，
①当x＞0时，由于在（0，+∞）上f（x）为增函数且f（1）=0，
∴由不等式f（x）≤0=f（1），得0＜x≤1；
②当x＜0时，-x＞0，
不等式f（x）≥0化成-f（x）≤0，即f（-x）≤0=f（1），
解之得-x≤1，即-1≤x＜0．
综上所述，原不等式的解集为[-1，0）∪（0，1]．
故答案为：[-1，0）∪（0，1]
∴f（x）-f（-x）=f（x）+f（x）=2f（x），
因此，不等式
| f(x)-f(-x) |
| x |
| 2f(x) |
| x |
化简得
|
|
①当x＞0时，由于在（0，+∞）上f（x）为增函数且f（1）=0，
∴由不等式f（x）≤0=f（1），得0＜x≤1；
②当x＜0时，-x＞0，
不等式f（x）≥0化成-f（x）≤0，即f（-x）≤0=f（1），
解之得-x≤1，即-1≤x＜0．
综上所述，原不等式的解集为[-1，0）∪（0，1]．
故答案为：[-1，0）∪（0，1]
练习册系列答案
相关题目
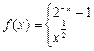
，若
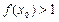，则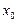
的取值范围是（ ） 
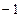，1）
）
，
）
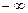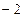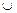（0，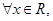
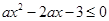恒成立”是真命题，则实数a的取值范围是 .
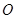为坐标原点，给定一个定点
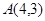，而点
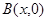在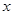
正半轴上移动，
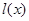表示
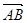的长，则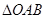
中两边长的比值
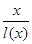的最大值为 ．