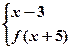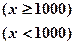题目内容
已知f(x+y)=f(x)+f(y),且f(1)=2,则f(1)+f(2)+…+f(n)不能等于( )
| A.f(1)+2f(1)+3f(1)+…+nf(1) | B.f[
| ||
| C.n(n+1) | D.n(n+1)f(1) |
令x=n,y=1,得f(n+1)=f(n)+f(1)=f(n)+2,
∴f(n+1)-f(n)=2,
可得{f(n)}构成以f(1)=2为首项,公差为2的等差数列,
∴f(n)=2+(n-1)×2=2n,
因此,f(1)+f(2)+…+f(n)=
=
=n(n+1)
对于A,由于f(1)+2f(1)+3f(1)+…+nf(1)
=f(1)(1+2+…+n)=2×
=n(n+1),故A正确;
对于B,由于f(n)=2n,所以f[
]=2×
=n(n+1),得B正确;
对于C,与求出的前n项和的通项一模一样,故C正确.
对于D,由于n(n+1)f(1)=2n(n+1),故D不正确.
故选:D
∴f(n+1)-f(n)=2,
可得{f(n)}构成以f(1)=2为首项,公差为2的等差数列,
∴f(n)=2+(n-1)×2=2n,
因此,f(1)+f(2)+…+f(n)=
| n[f(1)+f(n)] |
| 2 |
| n(2+2n) |
| 2 |
对于A,由于f(1)+2f(1)+3f(1)+…+nf(1)
=f(1)(1+2+…+n)=2×
| n(n+1) |
| 2 |
对于B,由于f(n)=2n,所以f[
| n(n+1) |
| 2 |
| n(n+1) |
| 2 |
对于C,与求出的前n项和的通项一模一样,故C正确.
对于D,由于n(n+1)f(1)=2n(n+1),故D不正确.
故选:D

练习册系列答案
相关题目
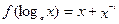 ,
,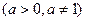
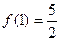 求
求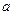 ;(2)证明
;(2)证明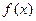 在
在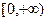 是增函数(14分)
是增函数(14分)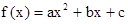 满足:
满足: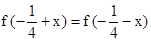 ,且
,且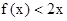 的
的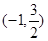
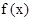 的解析式;
的解析式;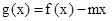
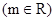 ,若
,若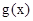 在
在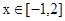 上的最小值为-4,求
上的最小值为-4,求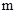 的值.
的值.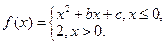 若
若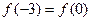 ,
,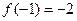 ,则关于
,则关于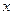 的方程
的方程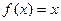 的解的个数为
的解的个数为  满足条件:
满足条件: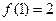 ,
,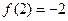 ,
,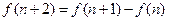 ,则
,则 的值为( )
的值为( )