��Ŀ����
����С��12�֣����壺������f��x�������䶨�����ڵ�ijһ��x0����f��x0��= x0�� ���x0��f��x����һ�������㣮��֪����f��x��=ax2+��b+1��x+b-1��a��0����
���x0��f��x����һ�������㣮��֪����f��x��=ax2+��b+1��x+b-1��a��0����
��1����a=1��b=-2ʱ������f��x���IJ����㣻
��2�����������ʵ��b������f��x���������������㣬��a��ȡֵ��Χ��
��3���ڣ�2���������£���y=f��x��ͼ����������A��B�ĺ������Ǻ���f��x���IJ����㣬��A��B�������ֱ��y=kx+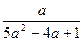 �Գƣ���b����Сֵ��
�Գƣ���b����Сֵ��
 ���x0��f��x����һ�������㣮��֪����f��x��=ax2+��b+1��x+b-1��a��0����
���x0��f��x����һ�������㣮��֪����f��x��=ax2+��b+1��x+b-1��a��0������1����a=1��b=-2ʱ������f��x���IJ����㣻
��2�����������ʵ��b������f��x���������������㣬��a��ȡֵ��Χ��
��3���ڣ�2���������£���y=f��x��ͼ����������A��B�ĺ������Ǻ���f��x���IJ����㣬��A��B�������ֱ��y=kx+
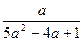 �Գƣ���b����Сֵ��
�Գƣ���b����Сֵ�� ������-1��3��������0<a<1��������bmin=-1
��1��f��x��=x2-x-3����x2-x-3=x����� x=3��-1��
��������IJ�����Ϊ-1��3�� ������������������3��
��2����ax2+��b+1��x+b-1=x����ax2+bx+b-1="0 " ��
�����⣬���̢ٺ�����������ʵ�������ԡ�=b2-4a��b-1��>0��
��b2-4ab+4a >0�������������������������������5��
>0�������������������������������5��
���¢=16a2-16a��0����0<a<1 ��������������������7��
��3����A��x1��x1����B��x2��x2����x1��x2������kAB=1����k=��1��
����y=-x+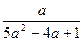 �� ����������������������������8��
�� ����������������������������8��
��AB���е��ڸ�ֱ���ϣ�����=��+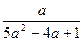 ��
��
��x1+x2=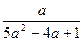 ��
��
��x1��x2Ӧ�Ƿ��̢ٵ�������������x1+x2=��������=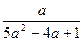 ��
��
��b=��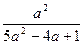 ��������������������������������10��
��������������������������������10��
=-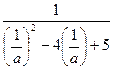 =-
=-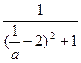
�൱ a=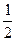 �ʣ�0��1��ʱ��bmin="-1 " ��������������������������12��
�ʣ�0��1��ʱ��bmin="-1 " ��������������������������12��
��������IJ�����Ϊ-1��3�� ������������������3��
��2����ax2+��b+1��x+b-1=x����ax2+bx+b-1="0 " ��
�����⣬���̢ٺ�����������ʵ�������ԡ�=b2-4a��b-1��>0��
��b2-4ab+4a
 >0�������������������������������5��
>0�������������������������������5�����¢=16a2-16a��0����0<a<1 ��������������������7��
��3����A��x1��x1����B��x2��x2����x1��x2������kAB=1����k=��1��
����y=-x+
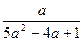 �� ����������������������������8��
�� ����������������������������8����AB���е��ڸ�ֱ���ϣ�����=��+
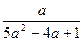 ��
����x1+x2=
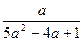 ��
����x1��x2Ӧ�Ƿ��̢ٵ�������������x1+x2=��������=
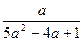 ��
����b=��
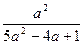 ��������������������������������10��
��������������������������������10��=-
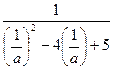 =-
=-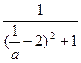
�൱ a=
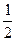 �ʣ�0��1��ʱ��bmin="-1 " ��������������������������12��
�ʣ�0��1��ʱ��bmin="-1 " ��������������������������12��
��ϰ��ϵ�д�
 ��У����ϵ�д�
��У����ϵ�д�
�����Ŀ
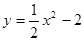 �ڵ�
�ڵ�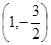 �������ߵ���б��Ϊ
�������ߵ���б��Ϊ



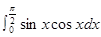 ����
����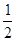
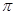
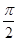
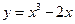 �ڵ�
�ڵ�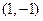 �������߷����ǣ� ����
�������߷����ǣ� ����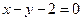
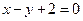
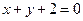
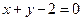
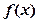 �ĵ�����Ϊ
�ĵ�����Ϊ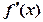 ��������
��������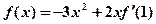 ����
����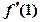 =�� ��
=�� ��
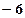
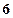
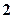
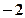
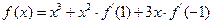 ����
����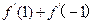 =
= 
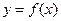 Ϊ
Ϊ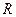 �ϵ������ɵ��ĺ�������
�ϵ������ɵ��ĺ�������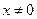 ʱ��
ʱ��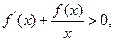 �����
�����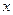 �ķ���
�ķ���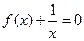 �ĸ��ĸ���Ϊ( )
�ĸ��ĸ���Ϊ( )